In which of the states shown in figure, is potential energy of a electric dipole maximum ?
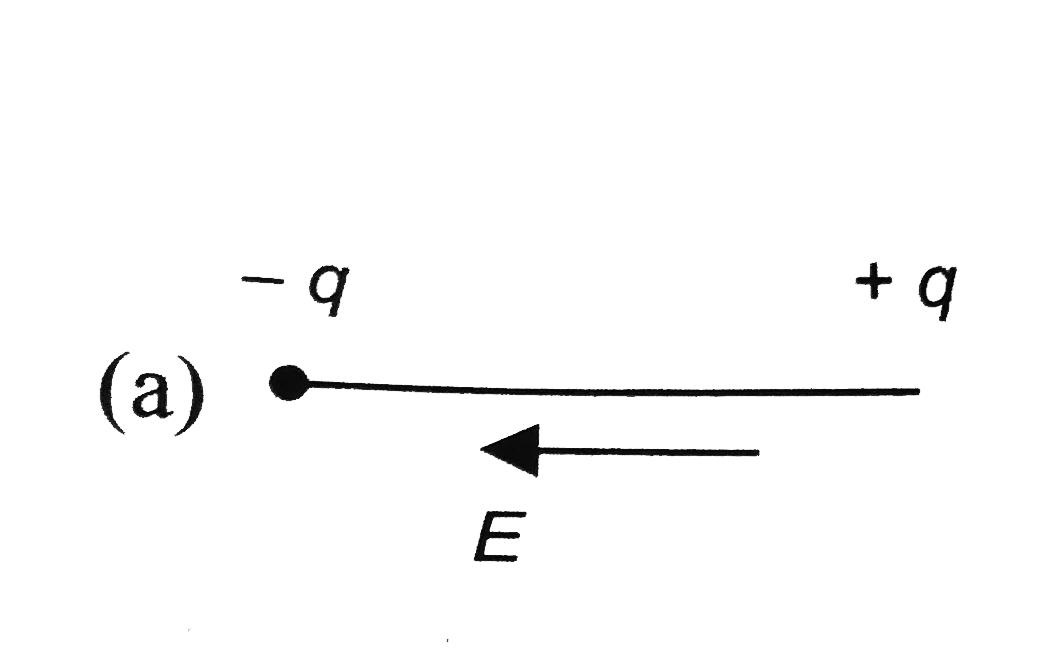

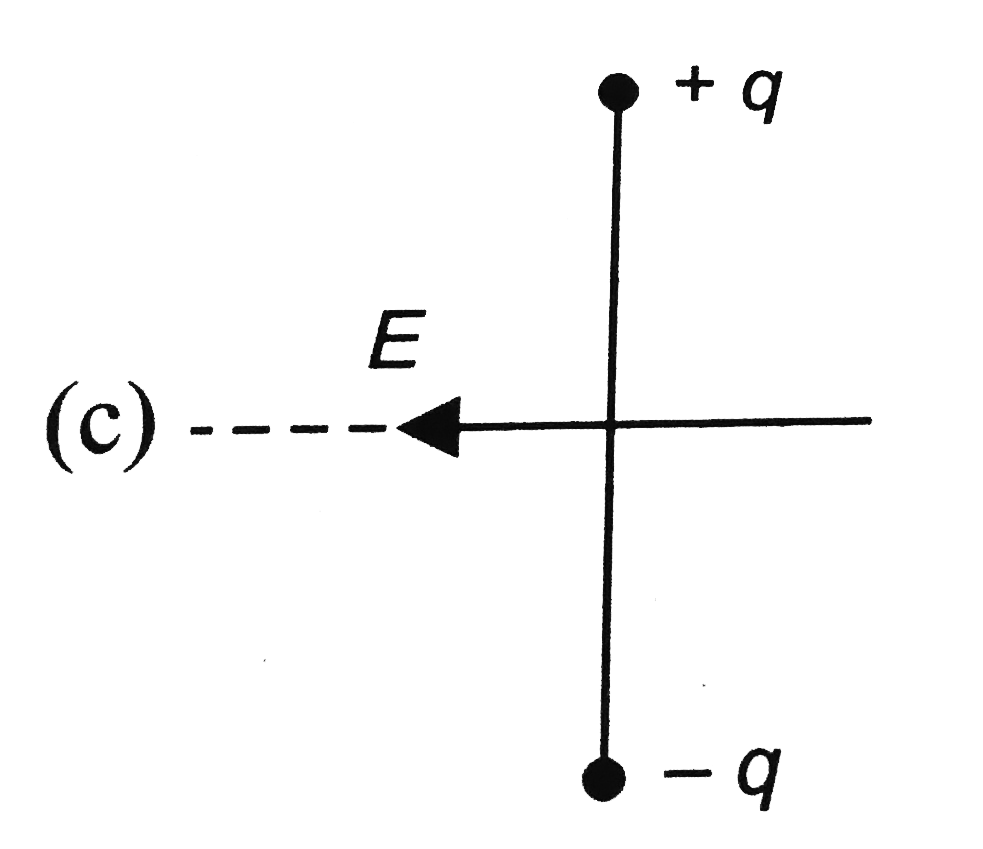

The correct Answer is:A
To determine in which state the potential energy of an electric dipole is maximum, we can follow these steps:
Step 1: Understand the formula for potential energy
The potential energy (U) of an electric dipole in an electric field is given by the formula:
U=−P⋅E=−PEcosθ
where:
- P is the magnitude of the dipole moment,
- E is the magnitude of the electric field,
- θ is the angle between the dipole moment and the electric field direction.
Step 2: Analyze the formula
From the formula U=−PEcosθ, we can see that:
- The potential energy is maximum when cosθ is at its minimum value.
- The minimum value of cosθ occurs when θ=180∘ (or π radians), which gives cos180∘=−1.
Step 3: Determine the maximum potential energy condition
When θ=180∘:
U=−PEcos180∘=−PE×(−1)=PE
This indicates that the potential energy is maximum when the dipole is aligned opposite to the electric field.
Step 4: Evaluate the given options
Now, we need to evaluate the orientations of the dipole in the provided figure (not shown here) to identify which orientation corresponds to θ=180∘.
1. If the dipole is aligned with the electric field (0 degrees): U=−PE
2. If the dipole is perpendicular to the electric field (90 degrees): U=0
3. If the dipole is opposite to the electric field (180 degrees): U=PE (maximum)
Step 5: Conclusion
The orientation of the dipole that corresponds to maximum potential energy is when it is aligned opposite to the direction of the electric field.
Final Answer
The potential energy of the electric dipole is maximum in the orientation where it is opposite to the electric field direction (typically represented as option A in the figure).
---
The potential energy (U) of an electric dipole in an electric field is given by the formula:
U=−P⋅E=−PEcosθ
where:
- P is the magnitude of the dipole moment,
- E is the magnitude of the electric field,
- θ is the angle between the dipole moment and the electric field direction.
From the formula U=−PEcosθ, we can see that:
- The potential energy is maximum when cosθ is at its minimum value.
- The minimum value of cosθ occurs when θ=180∘ (or π radians), which gives cos180∘=−1.
When θ=180∘:
U=−PEcos180∘=−PE×(−1)=PE
This indicates that the potential energy is maximum when the dipole is aligned opposite to the electric field.
Now, we need to evaluate the orientations of the dipole in the provided figure (not shown here) to identify which orientation corresponds to θ=180∘.
2. If the dipole is perpendicular to the electric field (90 degrees): U=0
3. If the dipole is opposite to the electric field (180 degrees): U=PE (maximum)
The orientation of the dipole that corresponds to maximum potential energy is when it is aligned opposite to the direction of the electric field.
The potential energy of the electric dipole is maximum in the orientation where it is opposite to the electric field direction (typically represented as option A in the figure).
Topper's Solved these Questions
Similar Questions
Knowledge Check
An electric dipole of moment p is palced in the positive of stable equilibrium in uniform electric field of intensity E. It is rotated through an angle θ from the initial position. The potential energy of electric dipole in the final position is
A−pEcosθBpE(−cosθ)CpEcosθDpEsinθAn electric dipole of moment p is placed in the positive of stable equilibrium in uniform electric field of intensity E. It is rotated through an angle θ from the initial position. The potential energy of electric dipole in the final position is
ApEcosθBpEsinθCpE(1−cosθ)D−pEcosθA dipole of electric dipole moment p is placed in a uniform electric field of strength E. If θ is the angle between positive direction of p and E, then the potential energy of the electric dipole is largest when θ is
Aπ4Bπ2CπDzero
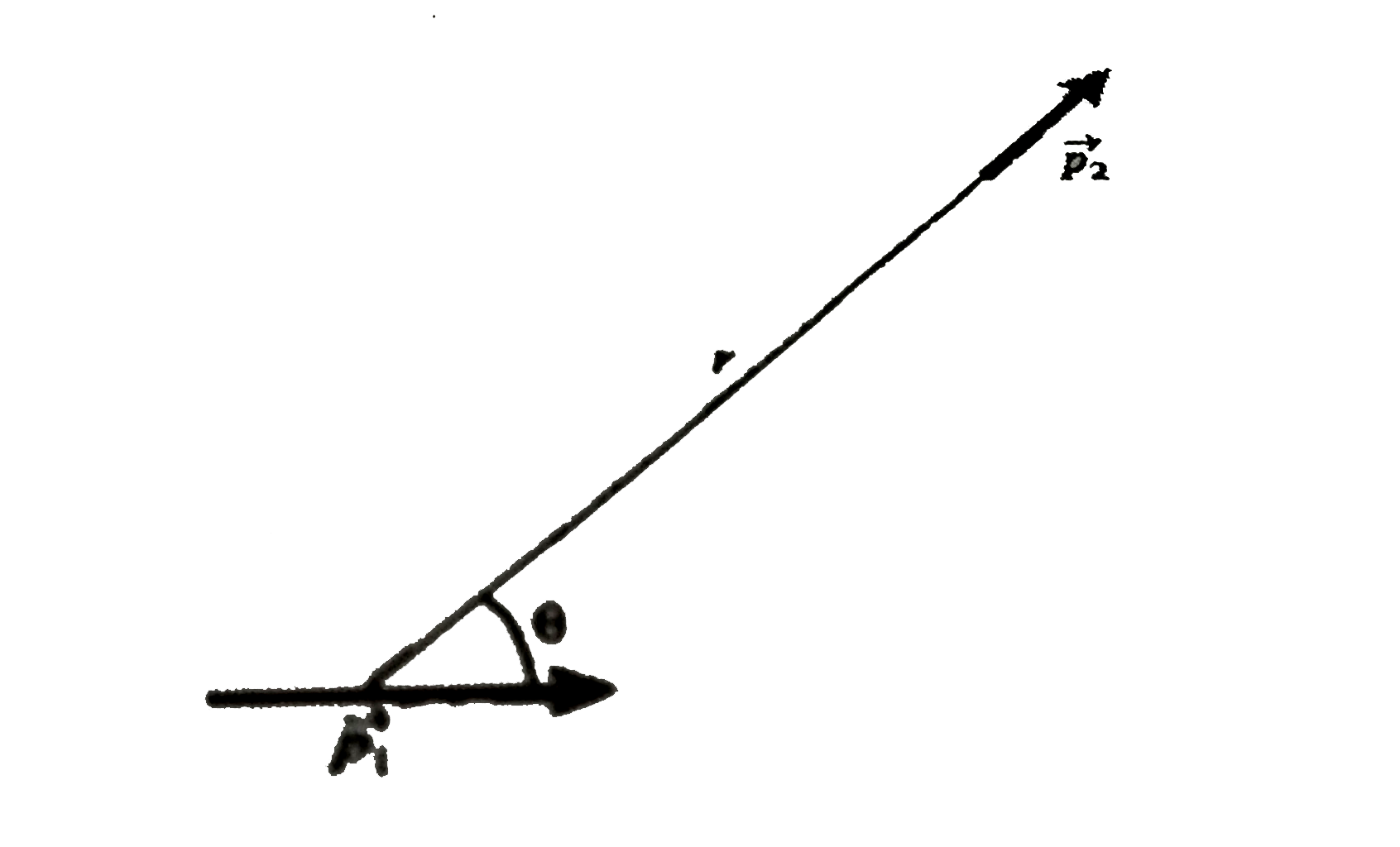
Two short electric dipoles are placed as shown in figure. Find the potential energy of electric interaction between these dipoles.
[−Kp1p2cosθr3]
View SolutionThe graph in figure-shows the potential energy of an electric dipole that oscillates between ±60∘. What is the kinetic energy of dipole when it is aligned with the field?
[1μJ]

View SolutionFind the expression of torque acting on an electric dipole placed in a uniform electric field . Using the above obtained expression of torque find the expression for potential energy of electric dipole kept in the uniform electric field . Assume potential energy of electric dipole to be zero when its axis is perpendicular to the externally applied electric field .
View SolutionDerive an expression for the potential energy of an electric dipole of dipole moment →p in an electric field →E.
View SolutionElectric potential Energy||Electric Potential
View Solution

