A mixture consists of two radioactive materials A1 and A2 with half-lives of 20s and 10s respectively. Initially the mixture has 40g of A1 and 160g of a2. The amount the two in the mixture will become equal after
40 s
60s
80 s
20 s
The correct Answer is:A
To solve the problem of when the amounts of two radioactive materials A1 and A2 will become equal, we can follow these steps:
Step 1: Understand the Problem
We have two radioactive materials:
- A1 with an initial amount of 40g and a half-life of 20s.
- A2 with an initial amount of 160g and a half-life of 10s.
We need to find the time t when the amounts of A1 and A2 will be equal.
Step 2: Write the Decay Formula
The amount of a radioactive substance remaining after time t can be calculated using the formula:
N(t)=N0(12)tT1/2
where:
- N(t) is the remaining quantity after time t,
- N0 is the initial quantity,
- T1/2 is the half-life of the substance.
Step 3: Set Up the Equations
For A1:
N1(t)=40(12)t20
For A2:
N2(t)=160(12)t10
Step 4: Set the Amounts Equal
We want to find t when N1(t)=N2(t):
40(12)t20=160(12)t10
Step 5: Simplify the Equation
Divide both sides by 40:
(12)t20=4(12)t10
Since 4=(12)−2, we can rewrite the equation as:
(12)t20=(12)−2(12)t10
This simplifies to:
(12)t20=(12)t10−2
Step 6: Equate the Exponents
Since the bases are the same, we can equate the exponents:
t20=t10−2
Step 7: Solve for t
Multiply through by 20 to eliminate the fractions:
t=2t−40
Rearranging gives:
t−2t=−40⟹−t=−40⟹t=40s
Conclusion
The time after which the amounts of A1 and A2 will become equal is 40s.
---
We have two radioactive materials:
- A1 with an initial amount of 40g and a half-life of 20s.
- A2 with an initial amount of 160g and a half-life of 10s.
The amount of a radioactive substance remaining after time t can be calculated using the formula:
N(t)=N0(12)tT1/2
where:
- N(t) is the remaining quantity after time t,
- N0 is the initial quantity,
- T1/2 is the half-life of the substance.
For A1:
N1(t)=40(12)t20
For A2:
N2(t)=160(12)t10
We want to find t when N1(t)=N2(t):
40(12)t20=160(12)t10
Divide both sides by 40:
(12)t20=4(12)t10
Since 4=(12)−2, we can rewrite the equation as:
(12)t20=(12)−2(12)t10
This simplifies to:
(12)t20=(12)t10−2
Since the bases are the same, we can equate the exponents:
t20=t10−2
Multiply through by 20 to eliminate the fractions:
t=2t−40
Rearranging gives:
t−2t=−40⟹−t=−40⟹t=40s
The time after which the amounts of A1 and A2 will become equal is 40s.
Topper's Solved these Questions
- NUCLEAR PHYSICSBook:A2ZChapter:NUCLEAR PHYSICSExercise:AIIMS Questions
Explore 22 Videos
- NUCLEAR PHYSICSBook:A2ZChapter:NUCLEAR PHYSICSExercise:Assertion- Reason
Explore 10 Videos
- NUCLEAR PHYSICSBook:A2ZChapter:NUCLEAR PHYSICSExercise:Section B - Assertion Reasoning
Explore 13 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Mock Test 3
Explore 44 Videos
- SEMICONDUCTOR ELECTRONICSBook:A2ZChapter:SEMICONDUCTOR ELECTRONICSExercise:EXERCISE
Explore 29 Videos
Similar Questions
In a radioactive decay processthe activity is defined as A = - (dN)/dtwhereN(t)istheνmberofradioactiveνc≤iattimet.Tworadioactivesources,S_1andS_2havesameactivityattimet=0.Atalatertime,theactivitiesofS_1andS_2areA_1andA_2,respectively.WhenS_1andS_2havejustcomp≤tedtheir3rdand7thhalf−lives,respectively,theratioA_1/A_2 is.
View Solution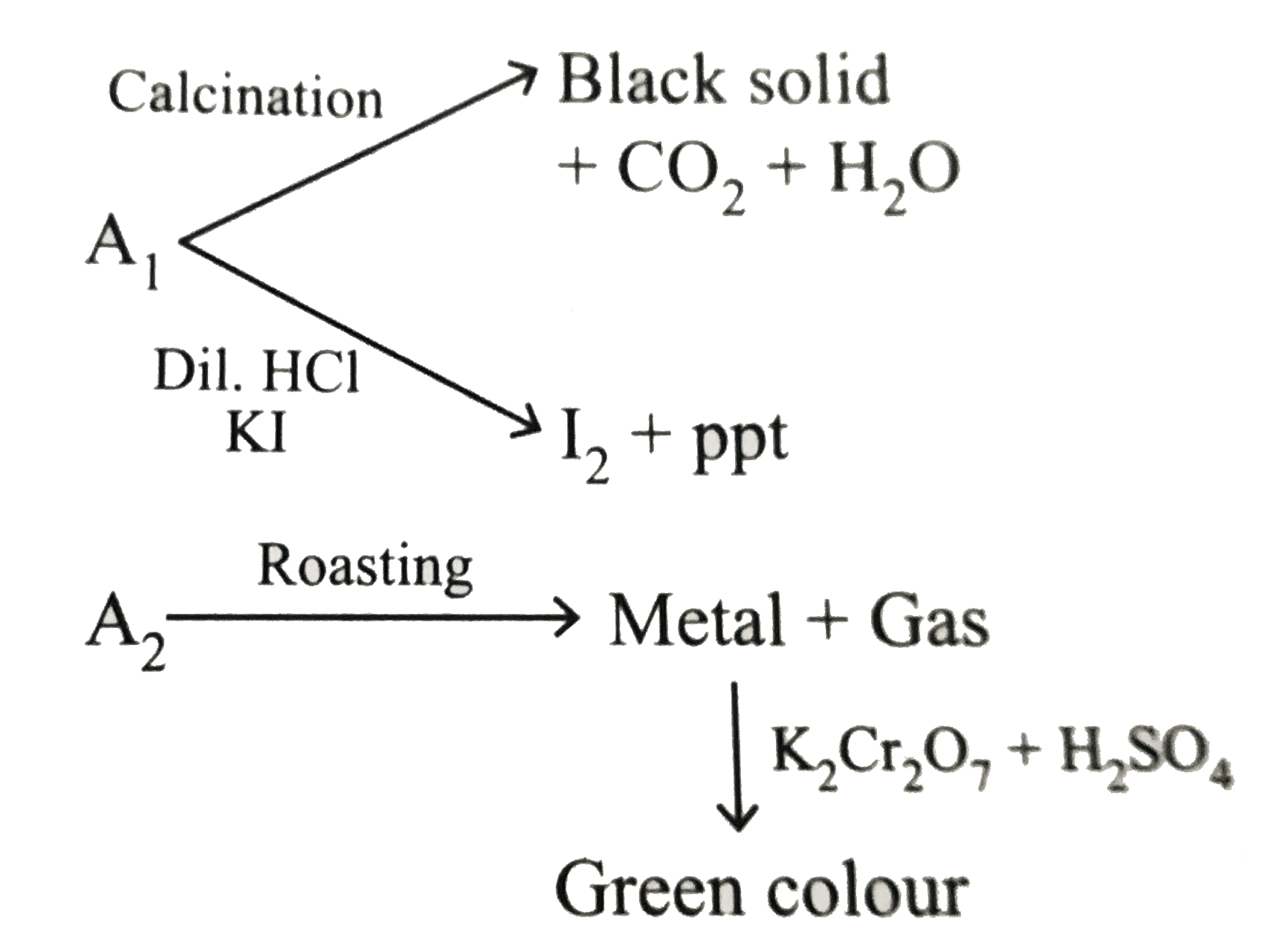
A1 and A2 are two ores of metal M.A1 on calcination gives black precipitate, CO2 and water. Identify A1 and A2.
View Solution
Knowledge Check
Atomic masses of two heavy atoms are A1 and A2. Ratio of their respective nuclear densities will be approximately
A(a) A1A2B(b) (A1A2)13C(c) (A2A1)13D(d) 1The decay constant of a radioactive isotope is λ. If A1 and A2 are its activities at time t1 and t2 respectively, then the number of nuclei which have decayed the time (t1−t2)
AA1t1−A2t2BA1−A2C(A1−A2)/λDλ(A1−A2)The ratio of nuclear density of two nuclei having mass number A1=12 and A2=14 is
A6:7B7:6C1:1D1:2
The pKa1 and pKa2 of an amino acid are 2.3 and 9.7 respectively. The isoelectric point of the amino acid is:
View SolutionTwo concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
View SolutionTwo wires of different materials of resistivity p1andp2 , length l1andl2, and area of cross-section A1andA2 respectively are connected in parallel. The ratio of current density in the two wires,j1j2 , is given by:
View SolutionThe activation energies of two reactions are Ea1 and Ea2 with Ea1>Ea2. If the temperature of the reacting systems is increased from T to T', which of the following is correct?
View SolutionThe activation energies of two reactions are Ea1 and Ea2 with Ea1>Ea2. If the temperature of the reacting systems is increased from T to T', which of the following is correct?
View Solution

