In the nth orbit, the energy of an electron $E_{n} = - \frac{13.6}{n^{2}} e V$ for hydrogen atom. The energy required to take the electron from first orbit to second orbit will be

A

$10.2 e V$

B

$12.1 e V$

C

$13.6 e V$

D

$3.4 e V$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

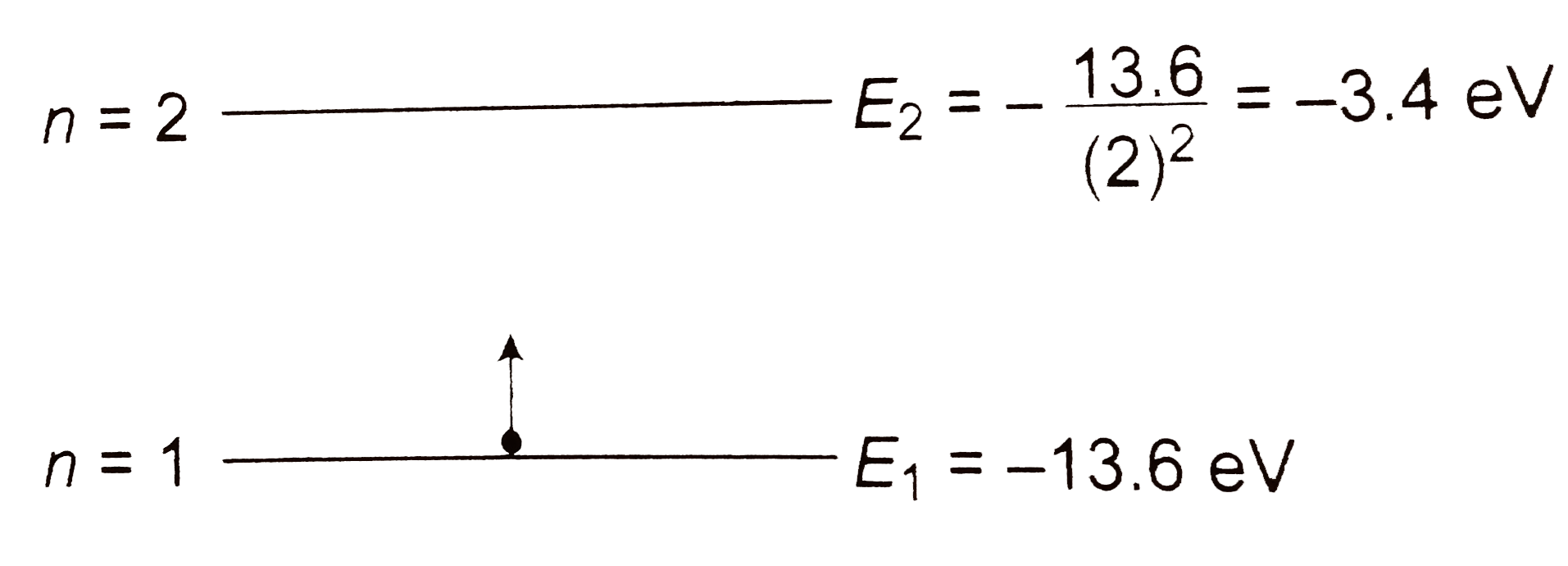
$E_{1 \to 2} = - 3.4 - (13.6) = + 10.2 e V$

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMS

Topper's Solved these Questions

BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Atomic Spectrum
53videos
ATOMIC PHYSICS
BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Problems Based On Mixed Concepts
43videos
ATOMIC PHYSICS
BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30videos
ATOMIC PHYSICS
BOOK - A2ZCHAPTER - ALTERNATING CURRENTEXERCISE - Section D - Chapter End Test
30videos
ALTERNATING CURRENT
BOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section D - Chapter End Test
29videos
CURRENT ELECTRICITY

Similar Questions

Knowledge Check

Question 1 - Select One
In the nth orbit, the energy of an electron $E_{n} = - \frac{13.6}{n^{2}} e V$ for hydrogen atom. The energy required to take the electron from first orbit to second orbit will be
A $10.2 e V$
B $12.1 e V$
C $13.6 e V$
D $3.4 e V$
Question 2 - Select One
In the nth stable orbit of a hydrogen atom, the energy of an electron $E = - \frac{13.6}{n^{2}}$ eV. The energy required to take the electron from first orbit to second orbit will be
A10.2 eV
B12.1 eV
C13.6 eV
D3.4 eV
Question 3 - Select One
Energy of the electron in $n t h$ orbit of hydrogen atom is given by $E_{n} = - \frac{13.6}{n^{2}} e V$ . The amount of energy needed to transfer electron from first orbit to third orbit is
A $13.6 e V$
B $3.4 e V$
C $12.09 e V$
D1.51 eV

A2Z-ATOMIC PHYSICS-Bohr'S Hydrogen Model

Home
Ask Doubt
Profile