A light of wavelength 5890Å falls normally on a thin air film. The min

A light of wavelength $5890 Å$ falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
A $2.945 \times 10^{- 7} m$
B $3.945 \times 10^{- 7} m$
C $4.95 \times 10^{- 7} m$
D $1.945 \times 10^{- 7} m$
A ray of light is incident at an angle of $45^{\circ}$ (ralative to the normal) on a thin film of a liquid with an index of refraction of $\sqrt{2}$ . Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.

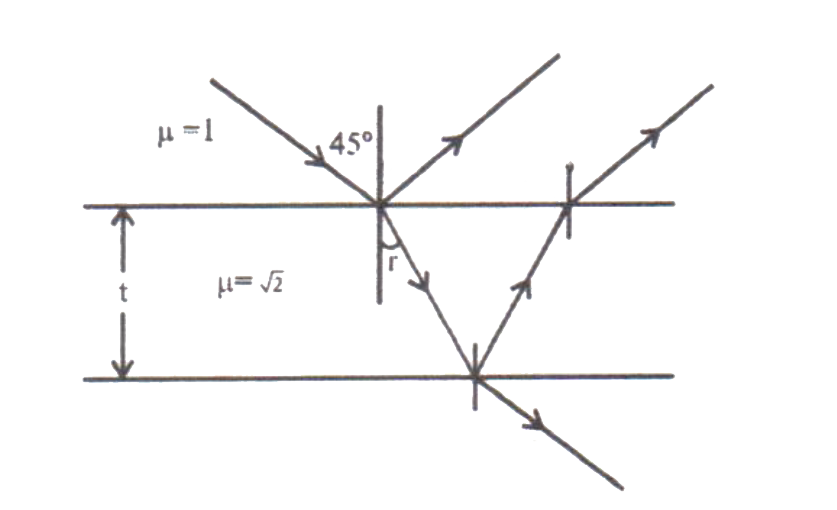A122 nm
B212 nm
C173 nm
D320 nm
A thin film of a specific meterial can be used to decrease the intensity of reflected light. There is destrucive inteference of wave reflected from upper and lower surface of the film. These films are called non-reflecting or anti-reflecting coatings. The process of coating the lens or surface with non-reflecting film is called blooming as shown in figure The refracting index of coating $(n_{1})$ is less than that of the glass $(n_{2})$ .

4. If a light of wavelength $λ$ is incident normally and the thickness of film is t, then optical path difference between waves reflected from upper and lower surface of the film is
A $2 n_{1} t$
B $2 n_{1} t - \frac{λ}{2}$
C $2 n_{1} t + \frac{λ}{2}$
D2 t

A light of wavelength $5890 Å$ falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is