Two identical radiators have a separation of $d = λ / 4$ where $λ$ is the wavelength of the waves emitted by either source. The initial phase difference between the sources is $λ / 4$ . Then the intensity on the screen at a distant point situated at an angle $θ = 30^{\circ}$ from the radiators is (here $I_{0}$ is intensity at that point due to one radiator alone)

(a) $I_{0}$

(b) $2 I_{0}$

(d) $4 I_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Two identical sources each of intensity $I_{0}$ have a separation $d = λ / 8$ , where $λ$ is the wavelength of the waves emitted by either source. The phase difference of the sources is $π / 4$ The intensity distribution $I (θ)$ in the radiation field as a function of $θ$ Which specifies the direction from the sources to the distant observation point P is given by
A $I (θ) = I_{0} {cos}^{2} θ$
B $I (θ) = \frac{I_{0}}{4} {cos}^{2} (\frac{π θ}{8})$
C $I (θ) = 4 I_{0} {cos}^{2} [\frac{π}{8} (sin θ + 1)]$
D $I (θ) = I_{0} {sin}^{2} θ$
Two point monochromatic and coherent sources of light of wavelength $λ$ are each placed as shown in the figure below. The initial phase difference between the sources is zero. Select the incorrect statement.

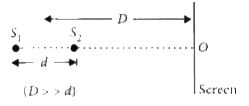AIf $d = \frac{7 λ}{2}$ , O will be minima
BIf $d = λ$ , only one maxima can be observed on screen .
CIf d=4.8 $λ$ , then total 10 minimas would be there on screen.
DIf $d = \frac{5 λ}{2}$ , then intensity at O would be maximum.
Two points nonochromatic and coherent sources of light of wavelength $λ$ each are placed as shown in figure. The initial phase difference between the sources is zero O. $(d > > d)$ . Mark the correct statement(s).

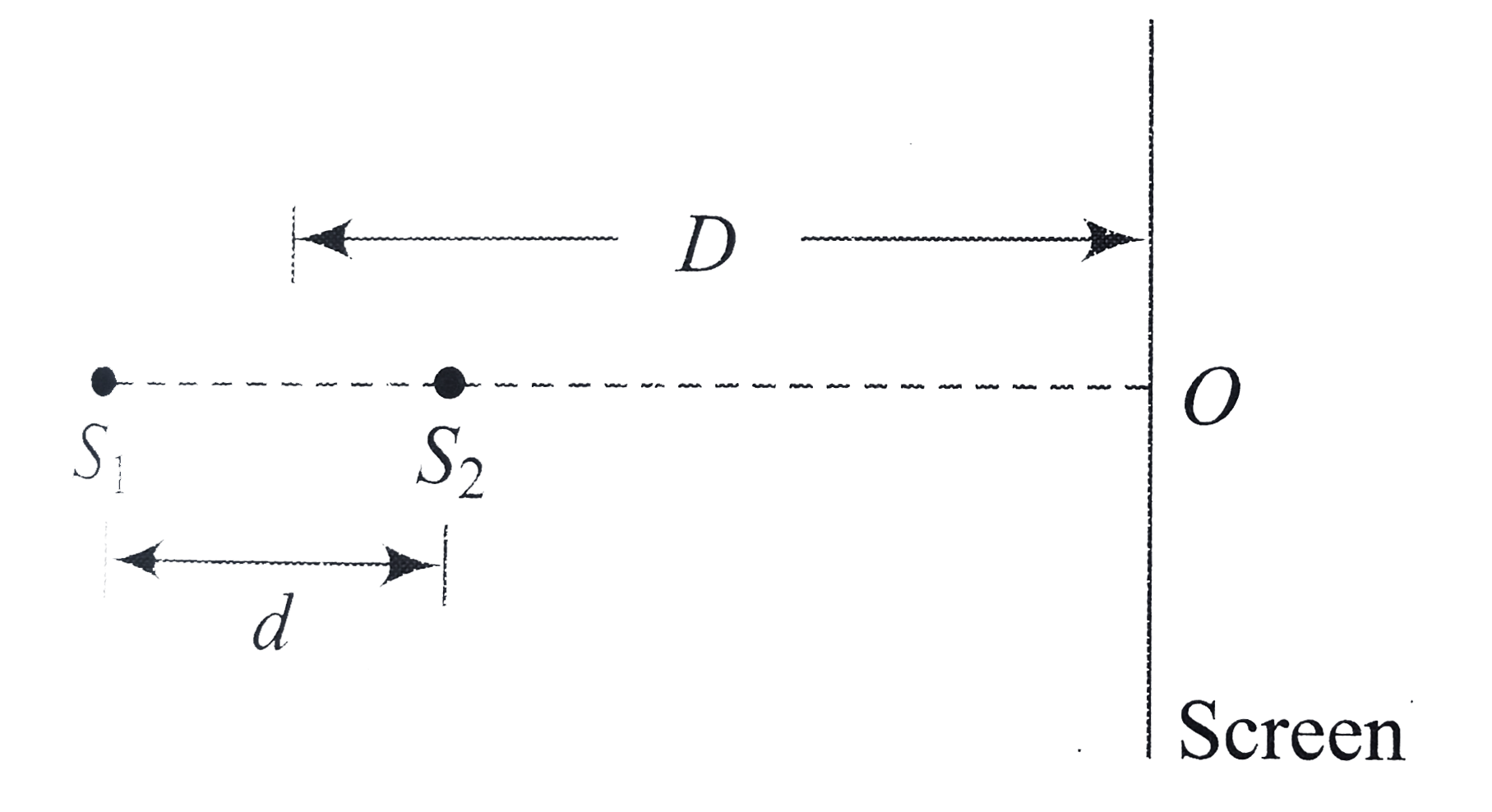AIf $d = \frac{7 λ}{2}$ , O will be a minima
BIf $d = λ$ , only one maxima can be observed on the screen
CIf $d = 4.8 λ$ , then total 10 minima would be there on the screen
DIf $d = \frac{5 λ}{2}$ , the intensity at O would be minimum.