Two identical thin planoconvex glass lenses (refractive index 1.5) each having radius of curvature of 20cm are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is
−20cm
−25cm
−50cm
50cm
The correct Answer is:C
Using lens maker's formula,
1f=(μ−1)(1R1−1R2)
1f1=(1.51−1)(1∞−1−20)
⇒f1=40cm
=1f2=(1.71−1)(1−20−1+20)
⇒f2=−1007cm
and 1f3=(1.51−1)(1∞−1−20)
⇒f3=40cm
1feq.=1f1+1f2=1f3
⇒1feq.=140+1−100/7+140
∴feq.=−50cm
Therefore, the focal length of the combination if −50cm.
Aliter :
Pconvex=μ−1R=1.5−120=140
Pconcave=2(1.7−1)R=2(0.7)20=7100
P=2Pconvex+Pconcave
=240−7100=10−14200=−4200=−150
F=−59cm
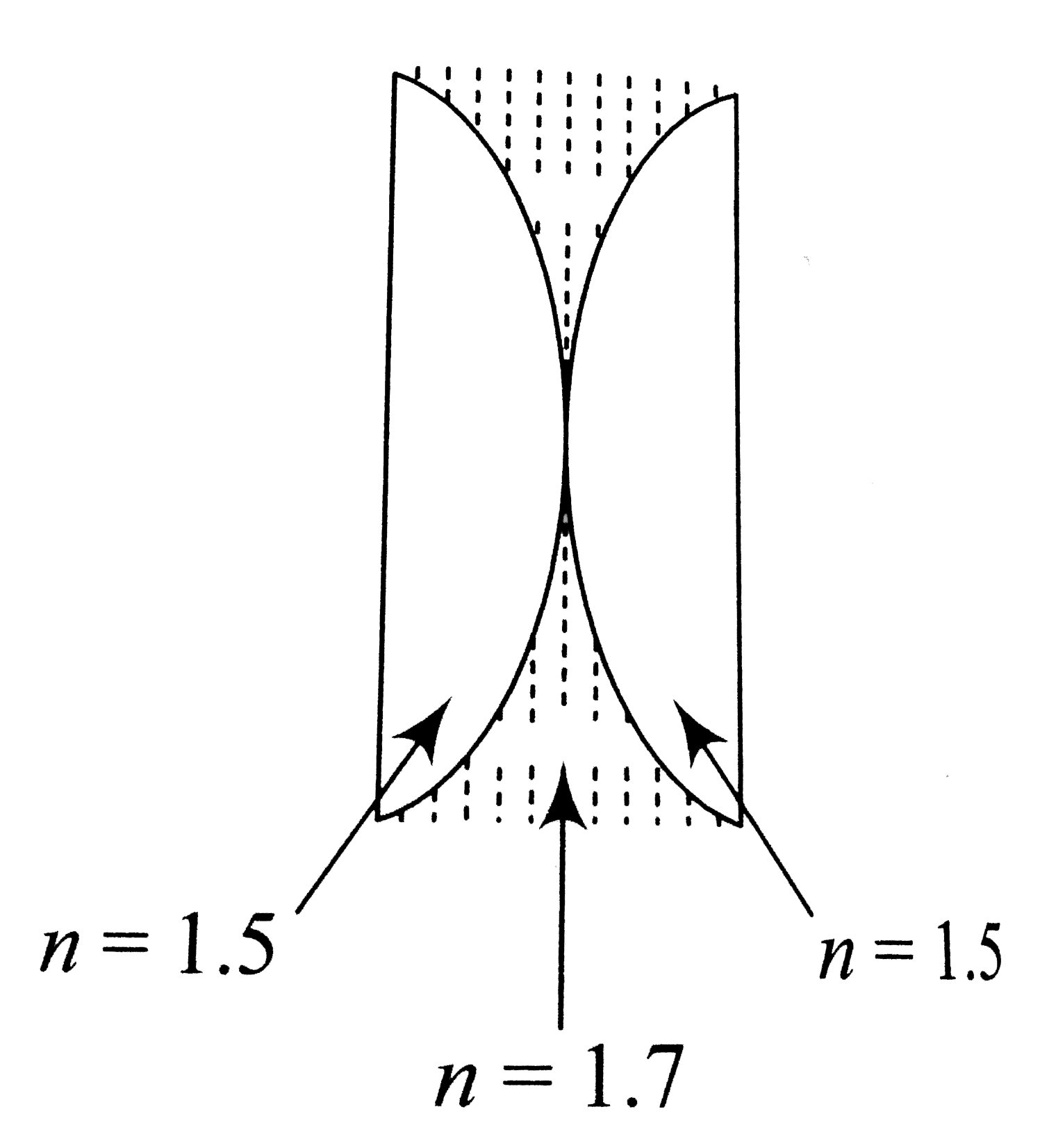
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion Reason
15 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section D - Chapter End Test
30 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section B - Assertion Reasoning
19 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Two plano concave lenses of glass of refractive index 1.5 have radii of currature 20cm and 30cm respectively. They are placed in contact with the curved surface to wards each other and the space between them is filled with a liquid of refractive index 3. The focal length of the combination is (in cm) (A) 12 (B) 16 (C) -92
View SolutionTwo plano concave lenses of glass of refractive index 1.5 have radii of currature 20cm and 30cm respectively.They are placed in contact with the curved surface to wards each other and the space between them is filled with a liquid of refractive index 52. The focal length of the combination is (in cm)
View Solution
Knowledge Check
Choose the most appropriate option.
Two identical thin plano-convex glass lenses (refractive index 1.5) each having radius of curvature of 20 cm are placed with their convex surfaces in contact at the center. The intervening space is lled with oil of refractive index 1.7. The focal length of the combination is:A−20cmB−25cmC−50cmD50 cmTwo identical thin planoconvex glass lenses (refractive index 1.5) each having radius of curvature of 20cm are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is
A−20cmsB−25cmC−50cmD50cmA concavo-convex lens has refractive index 1.5 and the radii of curvature of its surfaces are 10cmand20cm. The concave surface is upwards and is filled with oil of refractive index 1.6. The focal length of the combination will be
A18.18cmB15cmC22cmD28.57cm
Two plano-concave lenses of glass of refractive 1.5 have radii of curvature of 20 and 30 cm. They are placed in contact with curved surface towards each other and the space between yhem is filled with a liquid of refractive index 2/3. Find the focal length of the system.
View SolutionTwo plano-concave lenses of glass of refractive index 1.5 have radii of curvature of 20 and 30 cm. They are placed in contact with curved surface towards each other and the space between them is filled with a liquid of refractive index 43, find the focal length of the system.
View SolutionA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
View Solution
Two plano-concave lenses (1 and 2) of glass of refractive index 1.5 have radii of curvature 25 cm and 20 cm. They are placed in contact with their curved surface towards each other and the space betweent hem is filled with liquid of refractive index 43 the the combination is
View Solution
Two plano-concave lenses (1 and 2) of glass of refractive index 1.5 have radii of curvature 25 cm and 20 cm. They are placed in contact with their curved surface towards each other and the space betweent hem is filled with liquid of refractive index 43 the the combination is
View Solution
