An observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
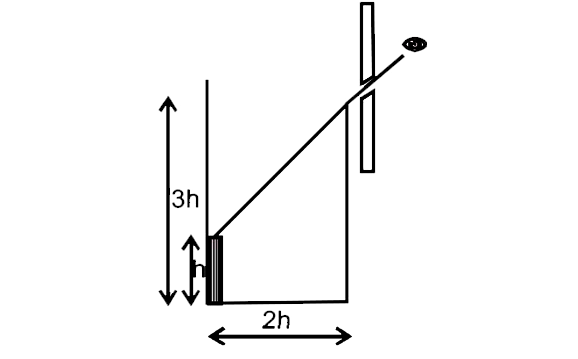
5/2
√(5/2)
√(3/2)
3/2
The correct Answer is:B
The line of sight of the observer remains constant, making an angle of 45∘ with the normal. sinθ=h√h2+(2h)2=1√5
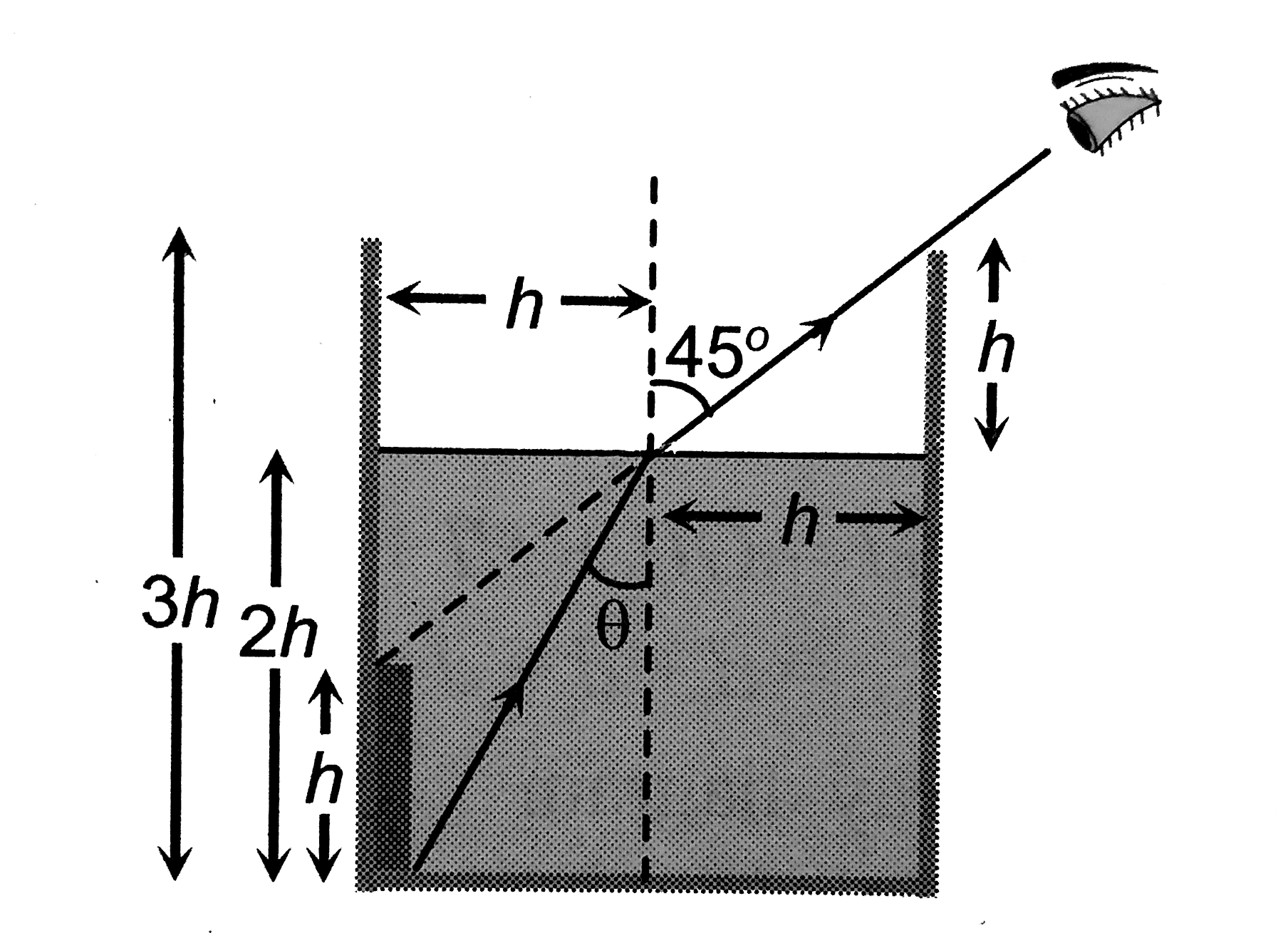
μ=sin45∘sinθ=1/√21/√5=√(52)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section B - Assertion Reasoning
19 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - AIPMT/NEET Questions
95 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Optical Instruments
55 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
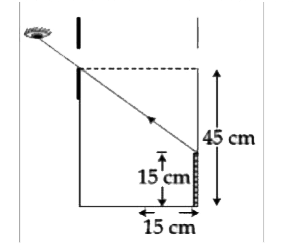
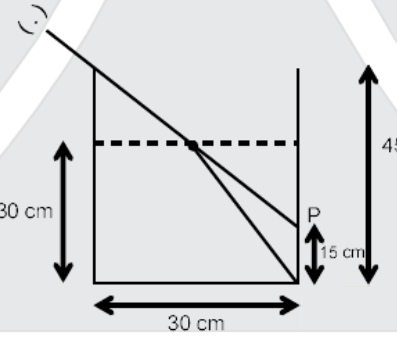
An observer can see through a small hole on the side of a jar (radius 15 cm) at a point at height of 15 cm from the bottom (see figure). The hole is at a height of 45 cm. When the jar is filled with a liquid up to a height of 30 cm the same observer can see the edge at the bottom of the jar. If the refractive index of the liquid is N/100, where N is an integer, the value of N is ___________.
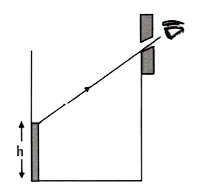
View SolutionA rod of height h is palced in a beaker of same radius. The height of the beaker is 3 times its radius. An observer sees the top end of the rod through a pin hole. When the beaker is filled with a liquid of refractive index √μ upto a height 2h, he can see the lower end of the rod. Find the value of μ
View Solution
Knowledge Check
An observer can see through a pin-hole the top end of a thin of height h, places as shown in figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
A52B√52C√32D32An observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
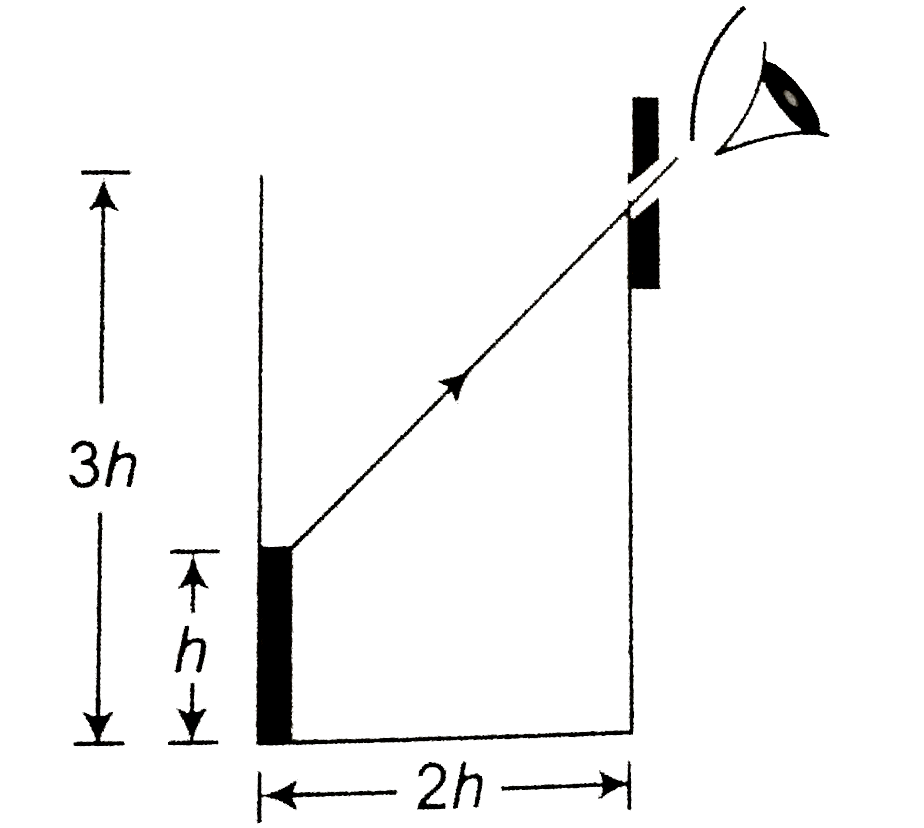A5/2B√(5/2)C√(3/2)D3/2A beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
A0BhρgChρg3D2hρg
An observers line of sight is at P, when container of diameter 30 cmand height 45 cm is empty.If this container is filled with liquid upto 30 cm height he is able to see the edge of container.Find refractive index of liquid.
View SolutionA cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.
Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external force
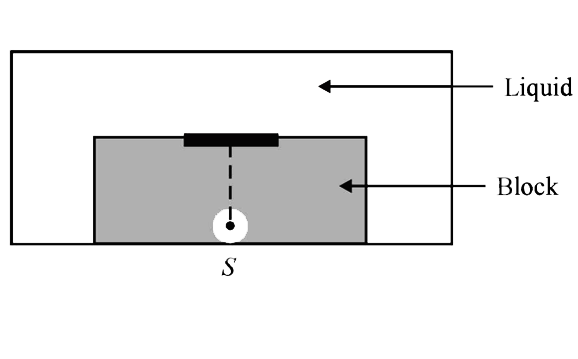
View SolutionA point source S is placed at the bottom of a tranparent block of height 10mm and refractive index 2.72. It is immersed in a lower refractive index liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter 11.54 mm on the top of the block. The refractive index of the liquid is
View SolutionA glass beaker has diameter 4cm wide at the bottom. An observer observes the edge of bottom when beaker is empty as shown in figure. When the beaker is completely filled with liquid of refractive index n=√5/2, he can just see the centre of bottom, then the height of glass beaker is :
View Solution