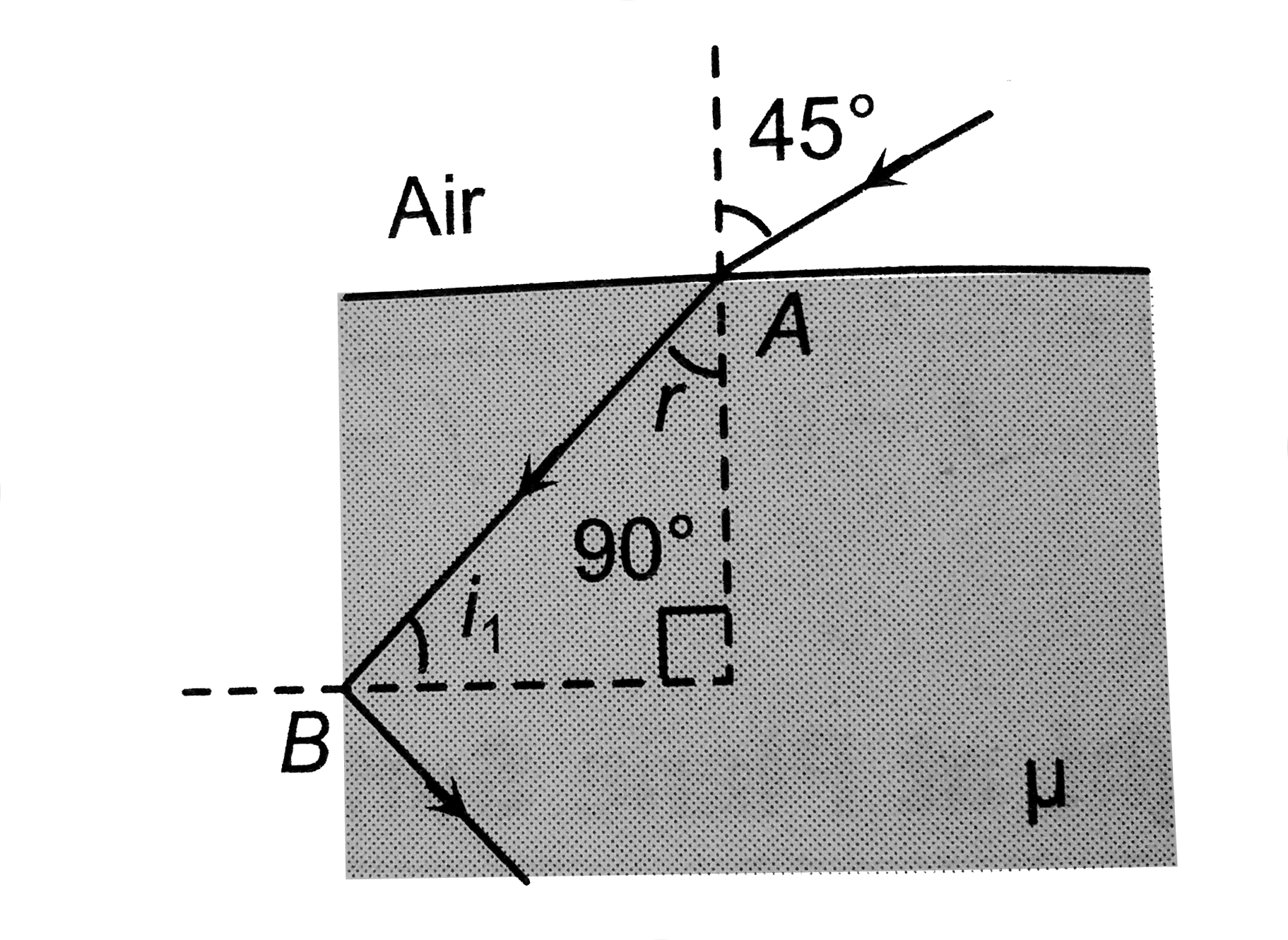
In the figure shown , for an angle of incidence $45^{\circ}$ , at the top surface , what is the minimum refractive index needed for the internal reflection at vertical face ?
$In the figure shown , for an angle of incidence 45^(@), at the top surface , what is the minimum refractive index needed for the internal reflection at vertical face ?$

$\frac{\sqrt{2} + 1}{2}$

$\sqrt{\frac{3}{2}}$

$\sqrt{\frac{1}{2}}$

$\sqrt{2} + 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

In the figure shown , for an angle of incidence $45^{\circ}$ , at the top surface , what is the minimum refractive index needed for the internal reflection at vertical face ?

A $\frac{\sqrt{2 + 1}}{2}$
B $\sqrt{3 / 2}$
C $\sqrt{1 / 2}$
D $\sqrt{2} + 1$
The angle of incidence on the surface of a diamond of refractive index 2.4, if the angle between the reflected and refracted rays is 90° is
A ${tan}^{- 1} (2.4)$
B $2 {sin}^{- 1} (\frac{1}{2.4})$
C ${tan}^{- 1} (\frac{1}{2.4})$
D ${cos}^{- 1} (\frac{1}{2.4})$
A light ray is incident on a transparent sphere of index = $\sqrt{2}$ , at an angle of incidence = $45^{\circ}$ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
A $270^{\circ}$
B $240^{\circ}$
C $120^{\circ}$
D $180^{\circ}$