Light wave enters from medium 1 to medium 2. Its velocity in 2nd medium is double from 1st. For total internal reflection, the angle of incidence must be greater than
30∘
60∘
45∘
90∘
The correct Answer is:A
To solve the problem of determining the angle of incidence for total internal reflection when light transitions from medium 1 to medium 2, we can follow these steps:
1. Understanding the Problem:
- We have two media: medium 1 and medium 2.
- The velocity of light in medium 2 (v2) is double that in medium 1 (v1), i.e., v2=2v1.
2. Finding the Refractive Indices:
- The refractive index (μ) of a medium is defined as the ratio of the speed of light in vacuum (c) to the speed of light in that medium.
- For medium 1, the refractive index μ1=cv1.
- For medium 2, the refractive index μ2=cv2=c2v1=12⋅cv1=12μ1.
3. Calculating the Critical Angle:
- Total internal reflection occurs when the angle of incidence exceeds the critical angle (ic).
- The critical angle can be found using Snell's law:
μ1sin(ic)=μ2sin(90∘)
- Since sin(90∘)=1, we can rewrite this as:
μ1sin(ic)=μ2
4. Substituting the Refractive Indices:
- We know μ2=12μ1, so substituting this into the equation gives:
μ1sin(ic)=12μ1
- Dividing both sides by μ1 (assuming μ1≠0):
sin(ic)=12
5. Finding the Critical Angle:
- Now we can find the critical angle ic:
ic=sin−1(12)
- This gives us:
ic=30∘
6. Conclusion:
- For total internal reflection to occur, the angle of incidence must be greater than the critical angle:
Angle of incidence must be greater than 30∘.
Final Answer:
The angle of incidence must be greater than 30∘.
---
- We have two media: medium 1 and medium 2.
- The velocity of light in medium 2 (v2) is double that in medium 1 (v1), i.e., v2=2v1.
- The refractive index (μ) of a medium is defined as the ratio of the speed of light in vacuum (c) to the speed of light in that medium.
- For medium 1, the refractive index μ1=cv1.
- For medium 2, the refractive index μ2=cv2=c2v1=12⋅cv1=12μ1.
- Total internal reflection occurs when the angle of incidence exceeds the critical angle (ic).
- The critical angle can be found using Snell's law:
μ1sin(ic)=μ2sin(90∘)
- Since sin(90∘)=1, we can rewrite this as:
μ1sin(ic)=μ2
- We know μ2=12μ1, so substituting this into the equation gives:
μ1sin(ic)=12μ1
- Dividing both sides by μ1 (assuming μ1≠0):
sin(ic)=12
- Now we can find the critical angle ic:
ic=sin−1(12)
- This gives us:
ic=30∘
- For total internal reflection to occur, the angle of incidence must be greater than the critical angle:
Angle of incidence must be greater than 30∘.
The angle of incidence must be greater than 30∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Refraction At Curved Surface
64 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Prism Theory And Dispersion Of Light
45 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
A sound wave travelling with a velocity V in a medium A reaches a point on the interface of medium A and medium B. If the velocity in the medium B be 2V, then the angle
of incidence for total internal reflection of the wave will be greater than:A15∘B30∘C45∘D90∘When a ray of light enters from one medium to another then its velocity in second medium becomes doubled. The maximum value of angle of incidence so that total internal reflection may not take place will be
A60∘B90∘C30∘D180∘In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction?
A90∘B180∘C0∘Dequal to angle of incidence
A light beam passes from medium 1 to medium 2. Show that the emerging beam is parallel to the incident beam.
View SolutionLight enters from vacuum to a medium of refractive index μ. If angle of incidence is double of angle of refraction, find angle of refraction.
View SolutionThe ray of light travels from raer medium to denser medium of refractive index μ. The angle of incidence of twice the angle of refraction. The angle of incidence is given by
View SolutionA light ray enters from medium A to medium B as shown in Figure. The refractive index of medium A relative to B will be
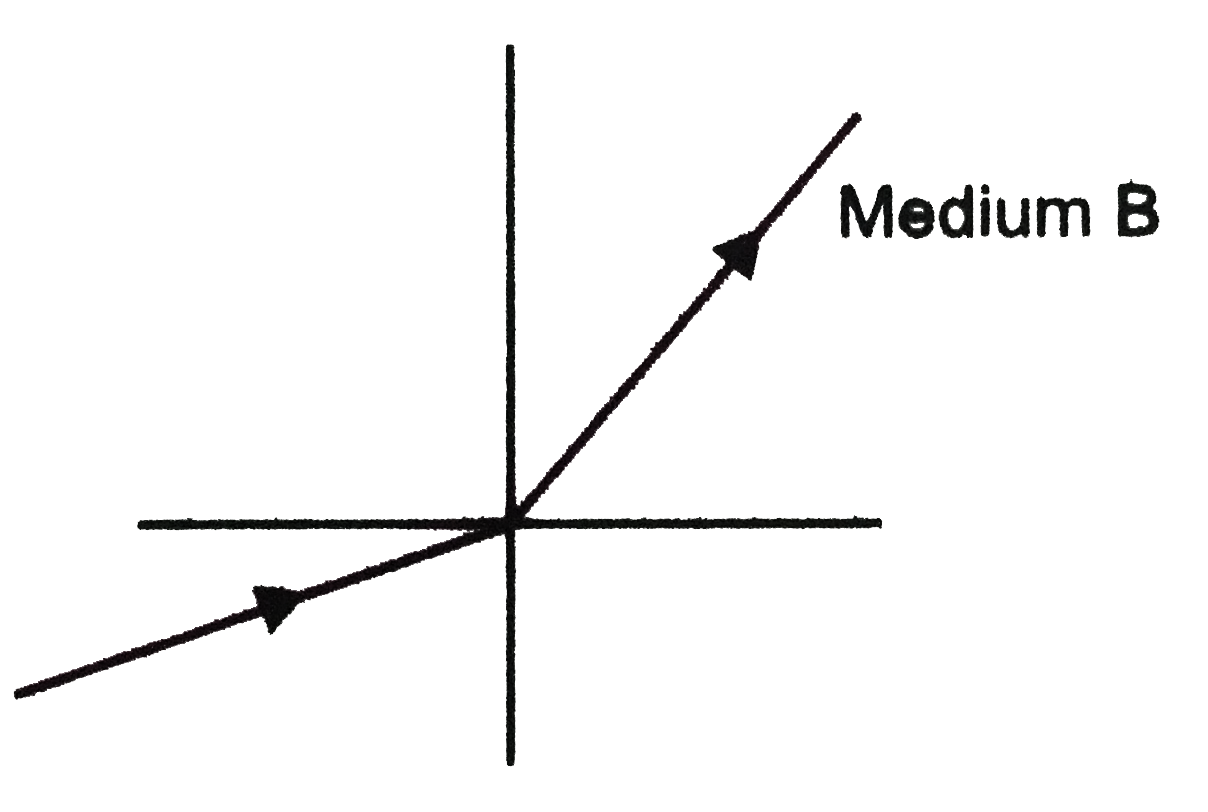
View SolutionA light ray enters from medium A to medium B as shown in Figure. The refractive index of medium A relative to B will be

View Solution