The length of the optical path of two media in contact of length d1 and d2 of refreactive indices μ1 and μ2 respectively, is
μ1d1+μ2d2
μ1d2+μ2d1
d1d2μ1μ2
d1+d2μ1μ2
The correct Answer is:A
To find the total length of the optical path when two media are in contact, we can follow these steps:
1. Understand the Concept of Optical Path Length:
The optical path length (OPL) is defined as the product of the refractive index of a medium and the physical length of the path traveled through that medium. Mathematically, it is given by:
Optical Path Length=μ×d
where μ is the refractive index and d is the physical length.
2. Identify the Two Media:
We have two media in contact:
- Medium 1 with refractive index μ1 and length d1
- Medium 2 with refractive index μ2 and length d2
3. Calculate the Optical Path Length for Each Medium:
- For Medium 1, the optical path length is:
OPL1=μ1×d1
- For Medium 2, the optical path length is:
OPL2=μ2×d2
4. Combine the Optical Path Lengths:
Since the two media are in contact, the total optical path length is the sum of the optical path lengths of both media:
Total Optical Path Length=OPL1+OPL2
Substituting the expressions we found:
Total Optical Path Length=μ1d1+μ2d2
5. Final Result:
Thus, the total length of the optical path when two media are in contact is:
Total Optical Path Length=μ1d1+μ2d2
The optical path length (OPL) is defined as the product of the refractive index of a medium and the physical length of the path traveled through that medium. Mathematically, it is given by:
Optical Path Length=μ×d
where μ is the refractive index and d is the physical length.
We have two media in contact:
- Medium 1 with refractive index μ1 and length d1
- Medium 2 with refractive index μ2 and length d2
- For Medium 1, the optical path length is:
OPL1=μ1×d1
- For Medium 2, the optical path length is:
OPL2=μ2×d2
Since the two media are in contact, the total optical path length is the sum of the optical path lengths of both media:
Total Optical Path Length=OPL1+OPL2
Substituting the expressions we found:
Total Optical Path Length=μ1d1+μ2d2
Thus, the total length of the optical path when two media are in contact is:
Total Optical Path Length=μ1d1+μ2d2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Refraction At Curved Surface
64 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Prism Theory And Dispersion Of Light
45 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A meniscus lens is made of a material of refractive index μ2.Both its surfaces have radii of curvature R.It has two different media of refractive indices μ1and μ3 respectively ,on its two sides (See figure) .Calcualte its focal length for μ1<μ2<μ3,when light is incidence on it as shown
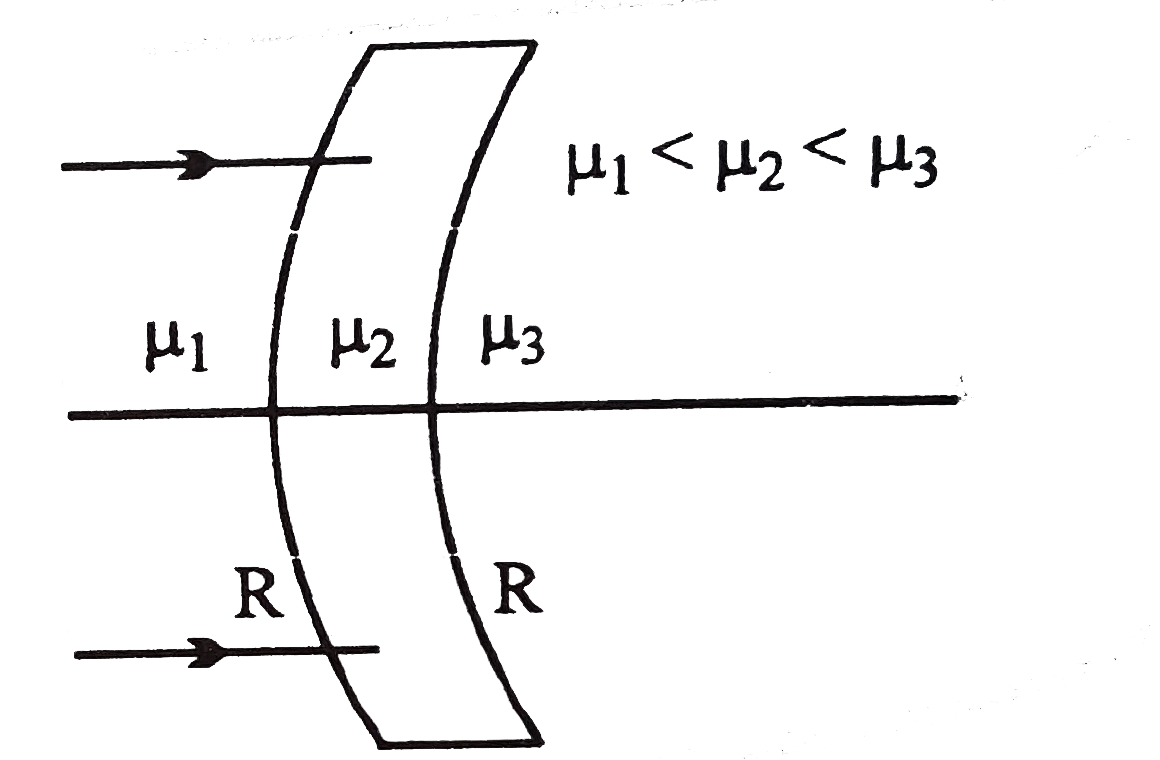
View SolutionIn a Young double slit experiment, the two slits are named as A and B. Two transparent films of thickness t1andt2 having refractive indices μ1 andμ2 placed in front of the slits A and B respectively. It is given that μ1t1=μ2t2 andt1<t2
In which direction will the central maximum shift after the two films are placed?
View Solution
Knowledge Check
The length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
Aμ1d1+μ2d2Bμ1d2+μ2d1Cd1d3μ1μ2Dd1+d2μ3μ2The length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
Aμ1d1+μ2d2Bμ1d2+μ2d1Cd1d2μ1μ2Dd1+d2μ1μ2A hollow double concave lens is made of very thin transparent material. It can be filled with air or either of two liquid L1 and L2 having refractive indices μ1 and μ2 respectively (μ2>μ1>1). The lens will diverge a parallel beam of light if it is filled with
Aair and placed in airBair and immersed in L1CL1 and immersed in L2DL2 and immersed in L1
If μ1andμ2are aboslute refractive index of medium 1 and medium 2 respectively, then
View SolutionIf refractive index of core & cladding are μ1 & μ2 respectively then :
View SolutionIf refractive index of core & cladding are μ1&μ2 respectively then :
View SolutionA hollow double concave lens is made of very thin transparent material. It can be filled with air or either of two liquids L_1 or L_2 having refractive indices mu_1 and mu_2 respectively (μ2>μ1>1). The lens will deverge a parallel beam of light if it is filled with
View SolutionIf a ray of light takes t1 and t2 times in two media of absolute refractive indices μ1 and μ2 respectively to travel same distance, then
View Solution
