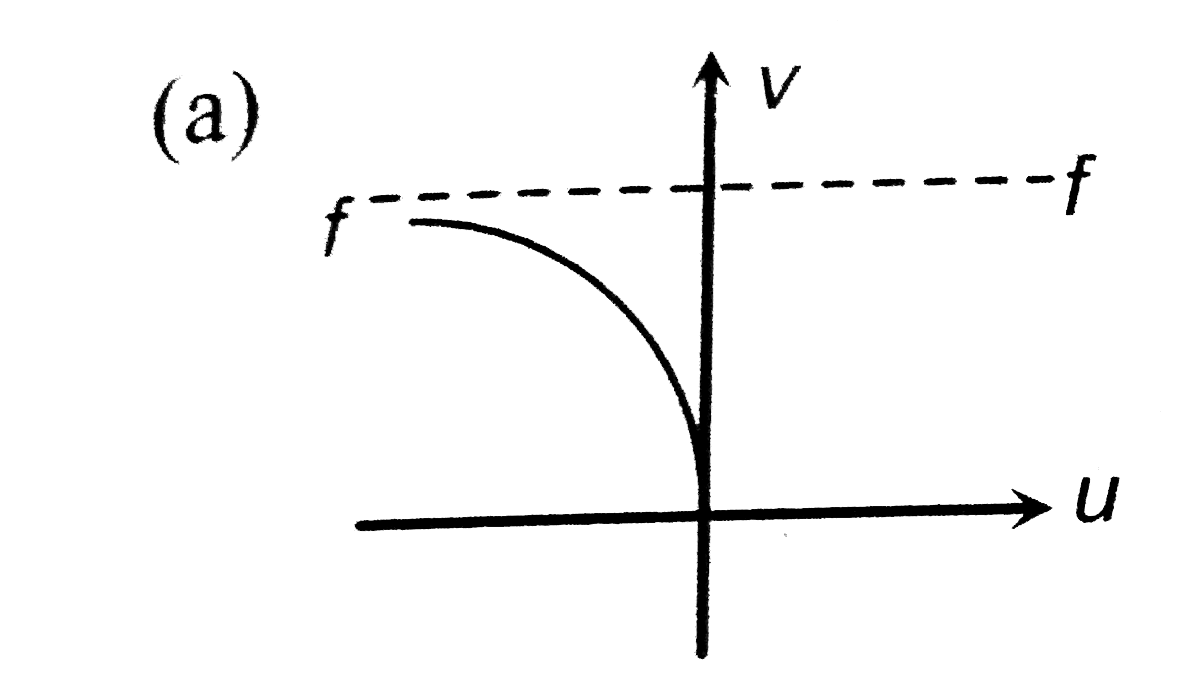
The graph between u and v for a convex mirrorr is
The correct Answer is:A
To determine the graph between u (object distance) and v (image distance) for a convex mirror, we can follow these steps:
1. Understanding the Convex Mirror:
- A convex mirror always forms a virtual image. The image is upright and diminished, regardless of the position of the object.
2. Sign Convention:
- For a convex mirror, the object distance u is taken as negative (since the object is on the same side as the incoming light).
- The image distance v is positive (since the image is formed on the opposite side of the mirror).
3. Behavior at Infinity:
- When the object is at a very large distance (approaching negative infinity, u=−∞), the rays coming from the object are parallel.
- These rays appear to diverge from the focus of the convex mirror, which is located behind the mirror. Thus, for u=−∞, the image distance v approaches the focal point f (which is a positive value).
4. Closer Object Position:
- As the object moves closer to the mirror (i.e., u increases towards 0 from negative values), the image distance v also increases.
- When the object is at the pole of the mirror (i.e., u=0), the image distance v also approaches 0.
5. Plotting the Graph:
- On the graph, the x-axis represents u (object distance) and the y-axis represents v (image distance).
- The graph starts from the point where u is at −∞ and v is at f, moving towards the point where u is 0 and v is also 0.
- The relationship is such that as u increases (becomes less negative), v also increases, showing a positive correlation.
6. Conclusion:
- The graph between u and v for a convex mirror will be a curve that starts from the point (−∞,f) and approaches the origin (0,0). This indicates that as the object distance increases (becomes less negative), the image distance also increases.
- A convex mirror always forms a virtual image. The image is upright and diminished, regardless of the position of the object.
- For a convex mirror, the object distance u is taken as negative (since the object is on the same side as the incoming light).
- The image distance v is positive (since the image is formed on the opposite side of the mirror).
- When the object is at a very large distance (approaching negative infinity, u=−∞), the rays coming from the object are parallel.
- These rays appear to diverge from the focus of the convex mirror, which is located behind the mirror. Thus, for u=−∞, the image distance v approaches the focal point f (which is a positive value).
- As the object moves closer to the mirror (i.e., u increases towards 0 from negative values), the image distance v also increases.
- When the object is at the pole of the mirror (i.e., u=0), the image distance v also approaches 0.
- On the graph, the x-axis represents u (object distance) and the y-axis represents v (image distance).
- The graph starts from the point where u is at −∞ and v is at f, moving towards the point where u is 0 and v is also 0.
- The relationship is such that as u increases (becomes less negative), v also increases, showing a positive correlation.
- The graph between u and v for a convex mirror will be a curve that starts from the point (−∞,f) and approaches the origin (0,0). This indicates that as the object distance increases (becomes less negative), the image distance also increases.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Refraction At Curved Surface
64 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Prism Theory And Dispersion Of Light
45 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
The graph between E and v is
A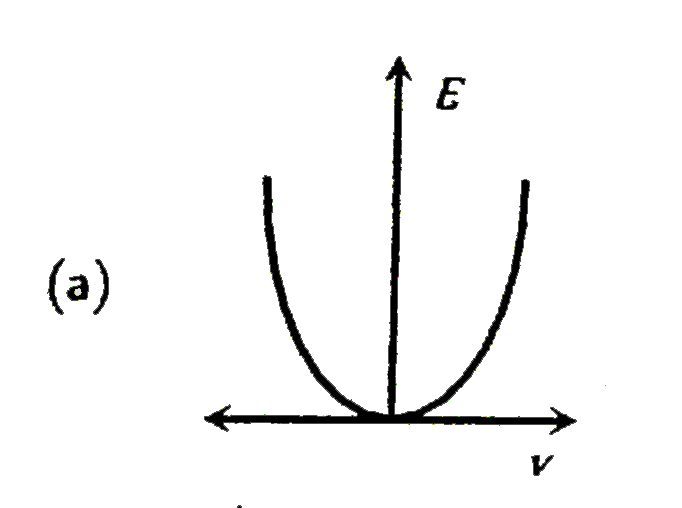 B
B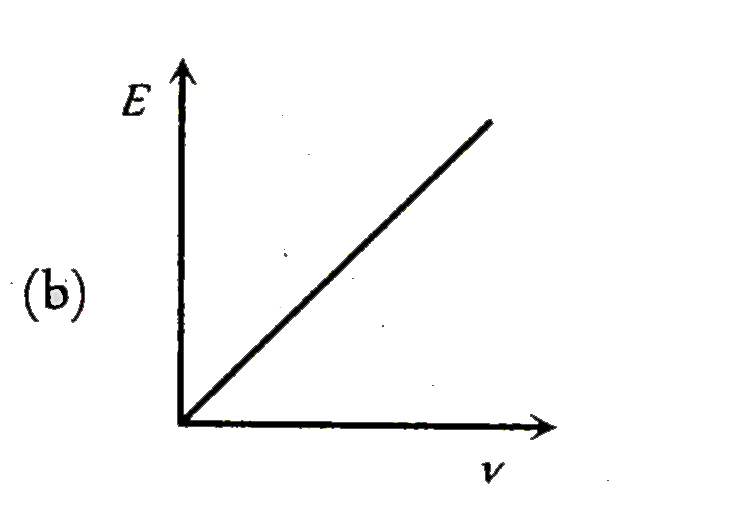 C
C D
D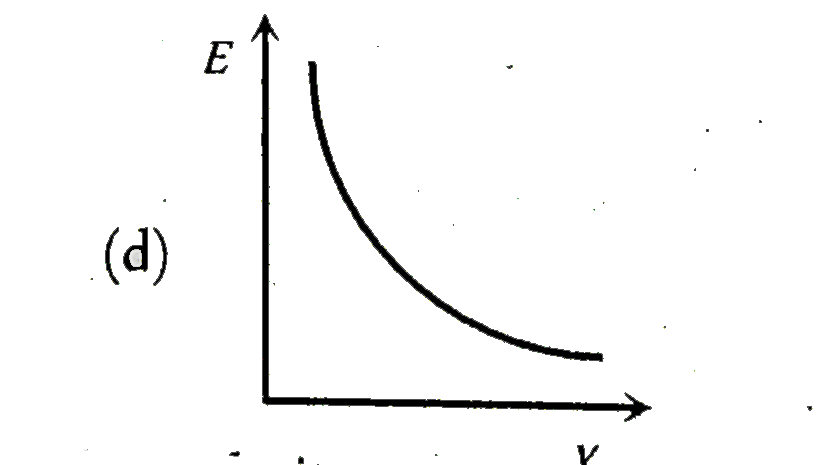
The graph between E and v is
A B
B C
C D
D
The graph between 1v and 1u for a concave mirror looks like.
A B
B C
C D
D
The shape of graph between 1/u and 1/v in case of a convex lens is Fig.
View SolutionFor a convex lens, if real image is formed the graph between (u+v) and u or v is as follows
View SolutionGraph between p and V at constant temperature is
View SolutionGraph between p and V at constant temperature is
View SolutionFor a convex lens, if real image is formed the graph between (u+v) and u or v is as follows
View Solution
