A series R−C circuit is connected to an alternating voltage source. Consider two situations
(a) When capacitor is air filled.
(b) When capacitor is mica filled.
current through resistor is i and voltage across capacitor is V then
Va=Vb
Va<Vb
Va>Vb
ia=ib
The correct Answer is:C
To solve the problem regarding the series R-C circuit connected to an alternating voltage source, we will analyze the two situations: when the capacitor is air-filled and when it is mica-filled.
1. Understanding the Circuit:
- We have an R-C series circuit connected to an alternating voltage source (V).
- The current through the resistor is denoted as i, and the voltage across the capacitor is denoted as VC.
2. Capacitance of Capacitors:
- For the air-filled capacitor (C_A), the capacitance is given by:
\(
C_A = \frac{\epsilon_0 A}{d}
\)
where \( \epsilon_0 \) is the permittivity of free space, \( A \) is the area of the plates, and \( d \) is the separation between the plates.
- For the mica-filled capacitor (C_B), the capacitance is given by:
\(
C_B = \epsilon_r \cdot C_A = \epsilon_r \cdot \frac{\epsilon_0 A}{d}
\)
where \( \epsilon_r > 1 \) (the relative permittivity of mica).
3. Comparing Capacitances:
- Since \( \epsilon_r > 1 \), it follows that:
\(
C_B > C_A
\)
4. Reactance of Capacitors:
- The capacitive reactance \( X_C \) is given by:
\(
X_C = \frac{1}{\omega C}
\)
- Therefore, for the air-filled capacitor:
\(
X_{C_A} = \frac{1}{\omega C_A}
\)
- And for the mica-filled capacitor:
\(
X_{C_B} = \frac{1}{\omega C_B}
\)
- Since \( C_B > C_A \), it follows that \( X_{C_B} < X_{C_A} \).
5. Impedance of the Circuit:
- The total impedance \( Z \) of the circuit is given by:
\(
Z = \sqrt{R^2 + X_C^2}
\)
- For the air-filled capacitor:
\(
Z_A = \sqrt{R^2 + X_{C_A}^2}
\)
- For the mica-filled capacitor:
\(
Z_B = \sqrt{R^2 + X_{C_B}^2}
\)
- Since \( X_{C_B} < X_{C_A} \), it follows that \( Z_B < Z_A \).
6. Current in the Circuit:
- The current \( i \) in the circuit can be expressed as:
\(
i = \frac{V}{Z}
\)
- Therefore:
\(
i_A = \frac{V}{Z_A} \quad \text{and} \quad i_B = \frac{V}{Z_B}
\)
- Since \( Z_B < Z_A \), it follows that \( i_B > i_A \).
7. Voltage Across the Capacitors:
- The voltage across the capacitor is given by:
\(
V_C = i \cdot X_C
\)
- For the air-filled capacitor:
\(
V_{C_A} = i_A \cdot X_{C_A}
\)
- For the mica-filled capacitor:
\(
V_{C_B} = i_B \cdot X_{C_B}
\)
- Since \( i_B > i_A \) and \( X_{C_B} < X_{C_A} \), we can conclude that:
\(
V_{C_B} < V_{C_A}
\)
Conclusion:
- Thus, we find that the voltage across the capacitor when it is air-filled is greater than when it is mica-filled:
\(
V_{C_A} > V_{C_B}
\)
Final Answer:
The correct option is that the voltage across the air-filled capacitor is greater than that across the mica-filled capacitor.
---
- We have an R-C series circuit connected to an alternating voltage source (V).
- The current through the resistor is denoted as i, and the voltage across the capacitor is denoted as VC.
- For the air-filled capacitor (C_A), the capacitance is given by:
\(
C_A = \frac{\epsilon_0 A}{d}
\)
where \( \epsilon_0 \) is the permittivity of free space, \( A \) is the area of the plates, and \( d \) is the separation between the plates.
- For the mica-filled capacitor (C_B), the capacitance is given by:
\(
C_B = \epsilon_r \cdot C_A = \epsilon_r \cdot \frac{\epsilon_0 A}{d}
\)
where \( \epsilon_r > 1 \) (the relative permittivity of mica).
- Since \( \epsilon_r > 1 \), it follows that:
\(
C_B > C_A
\)
- The capacitive reactance \( X_C \) is given by:
\(
X_C = \frac{1}{\omega C}
\)
- Therefore, for the air-filled capacitor:
\(
X_{C_A} = \frac{1}{\omega C_A}
\)
- And for the mica-filled capacitor:
\(
X_{C_B} = \frac{1}{\omega C_B}
\)
- Since \( C_B > C_A \), it follows that \( X_{C_B} < X_{C_A} \).
- The total impedance \( Z \) of the circuit is given by:
\(
Z = \sqrt{R^2 + X_C^2}
\)
- For the air-filled capacitor:
\(
Z_A = \sqrt{R^2 + X_{C_A}^2}
\)
- For the mica-filled capacitor:
\(
Z_B = \sqrt{R^2 + X_{C_B}^2}
\)
- Since \( X_{C_B} < X_{C_A} \), it follows that \( Z_B < Z_A \).
- The current \( i \) in the circuit can be expressed as:
\(
i = \frac{V}{Z}
\)
- Therefore:
\(
i_A = \frac{V}{Z_A} \quad \text{and} \quad i_B = \frac{V}{Z_B}
\)
- Since \( Z_B < Z_A \), it follows that \( i_B > i_A \).
- The voltage across the capacitor is given by:
\(
V_C = i \cdot X_C
\)
- For the air-filled capacitor:
\(
V_{C_A} = i_A \cdot X_{C_A}
\)
- For the mica-filled capacitor:
\(
V_{C_B} = i_B \cdot X_{C_B}
\)
- Since \( i_B > i_A \) and \( X_{C_B} < X_{C_A} \), we can conclude that:
\(
V_{C_B} < V_{C_A}
\)
- Thus, we find that the voltage across the capacitor when it is air-filled is greater than when it is mica-filled:
\(
V_{C_A} > V_{C_B}
\)
The correct option is that the voltage across the air-filled capacitor is greater than that across the mica-filled capacitor.
Topper's Solved these Questions
- ALTERNATING CURRENTBook:A2ZChapter:ALTERNATING CURRENTExercise:AIIMS Questions
Explore 26 Videos
- ALTERNATING CURRENTBook:A2ZChapter:ALTERNATING CURRENTExercise:Section D - Chapter End Test
Explore 30 Videos
- ALTERNATING CURRENTBook:A2ZChapter:ALTERNATING CURRENTExercise:Section B - Assertion Reasoning
Explore 26 Videos
- ATOMIC PHYSICSBook:A2ZChapter:ATOMIC PHYSICSExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
In a series CR circuit shown in figure,the applied voltage is 10V and the voltage across capacitor is found to be 8V
View SolutionA series circuit consisting of a capacitor XC=80Ω and a coil with active resistance R=300Ω and inductance XL=40ω is connected to a source of alternating voltage with amplitude V0=200V Find
(a) the current amplitude in the circuit
(b) the phase difference between the current and voltage
(c) the amplitudes of voltage across the capacitor and the coli .
View Solution
Knowledge Check
A series R−C circuit is connected to an alternating voltage source. Consider two situations
(a) When capacitor is air filled.
(b) When capacitor is mica filled.
current through resistor is i and voltage across capacitor is V thenAVa=VbBVa<VbCVa>VbDia=ibA sereis R-C circuit is connected to AC voltage source. Consider two cases, (A) when C is without a dielectric medium and (B) when C is filled with dielectric of constant 4. The current IR through the resistor and voltage Vc across the capacitor are compared in the two cases. Which of the following is/ are true?
AIAR>IBRBIAR<IBRCVCA>VCBDVCA>VCBThe circuit shown has been connected for a long time. The voltage across the capacitor is
 A1.2VB2.0 VC2.4VD4.0 V
A1.2VB2.0 VC2.4VD4.0 V
A variable capacitor and an inductive coil with negligible resistance are connected in series to an A.C. voltage of value 100V. The current in the circuit is 5A. When the capacitor decreases to half its value, the current becomes 10A. The voltage across the capacitor, in first case, is
View Solutioncircuit consists of a source of EMF ξ and internal resistance r, two capacitors each of capacitance C and two resistors, each of value R. The voltage across either capacitor is:

View SolutionA 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
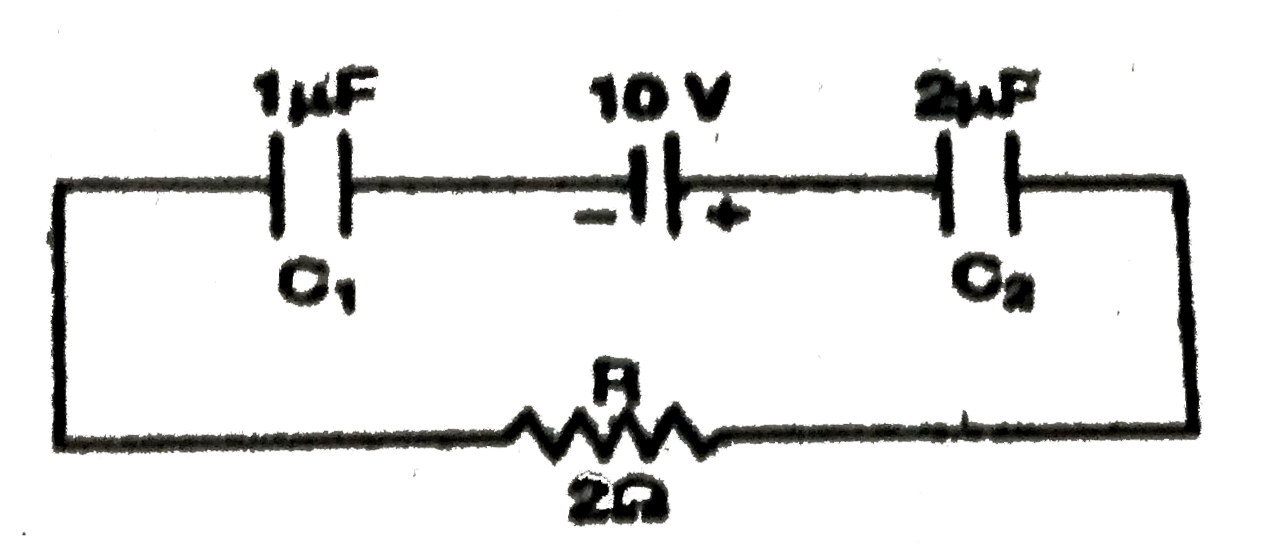
View SolutionAn LCR series circuit is connected to an oscillator (AC supply) having RMS voltage 200 V. If the RMS voltages across resistor, inductor and capacitor are equal, then RMS voltage across the resistor would be
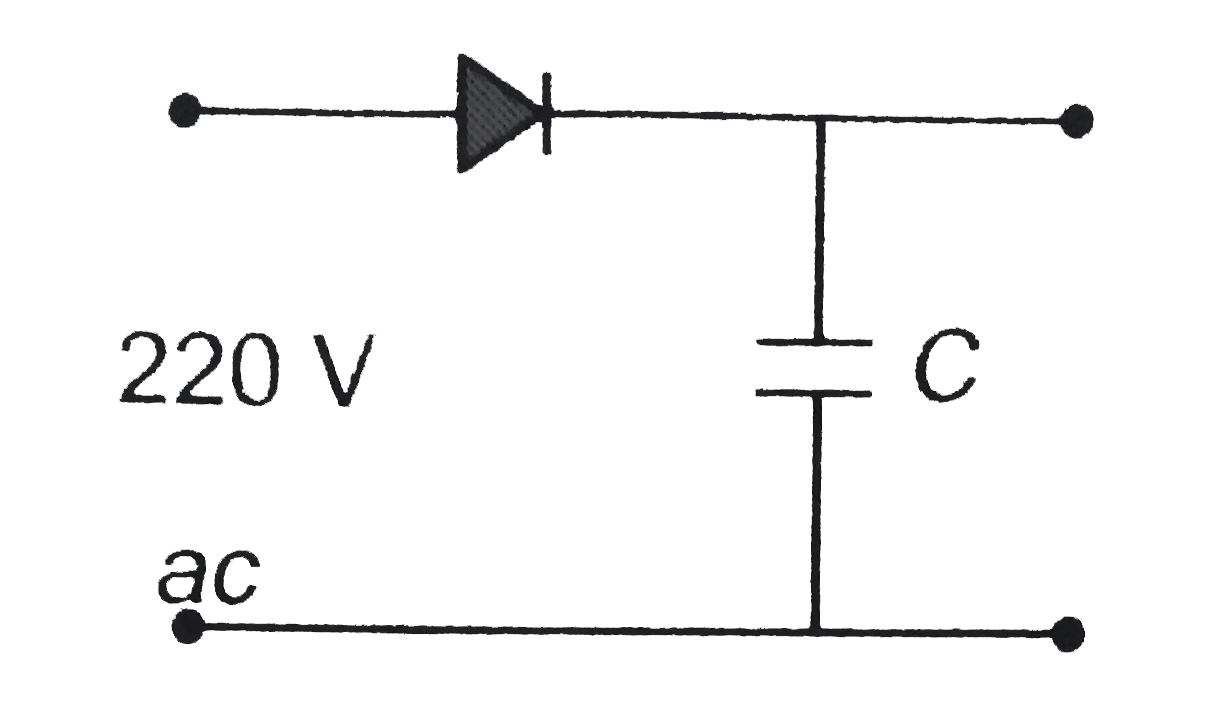
View SolutionA diode is connected to 220V(rms) ac in series with a capacitor as shown in fig. The voltage across the capacitor is
View Solution

