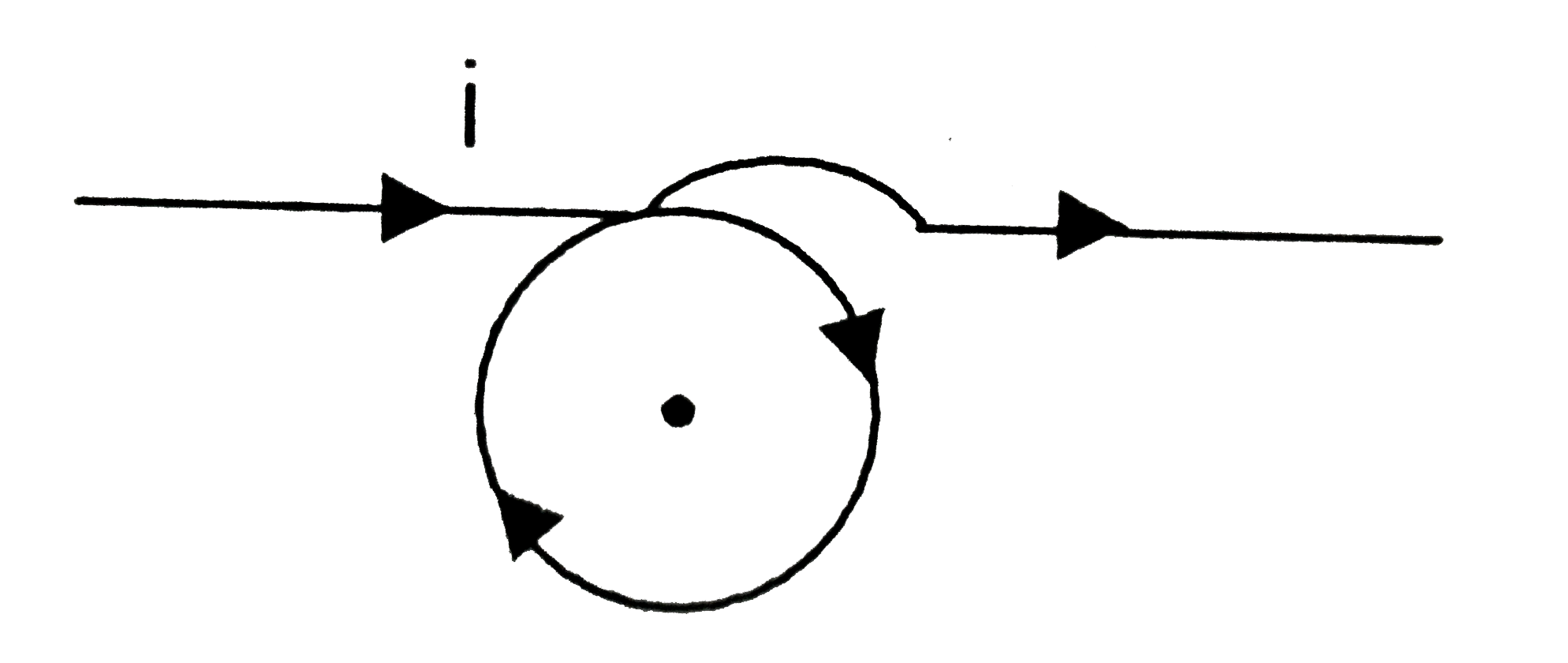
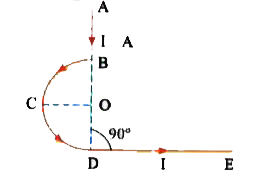
In the given figure net magnetic field at O will be
A
2μ0i3πa√4−π2
B
μ0i3πa√4+π2
C
2μ0i3πa2√4+π2
D
μ0i3πa√(4+π2)
Video Solution
Text Solution
The correct Answer is:B
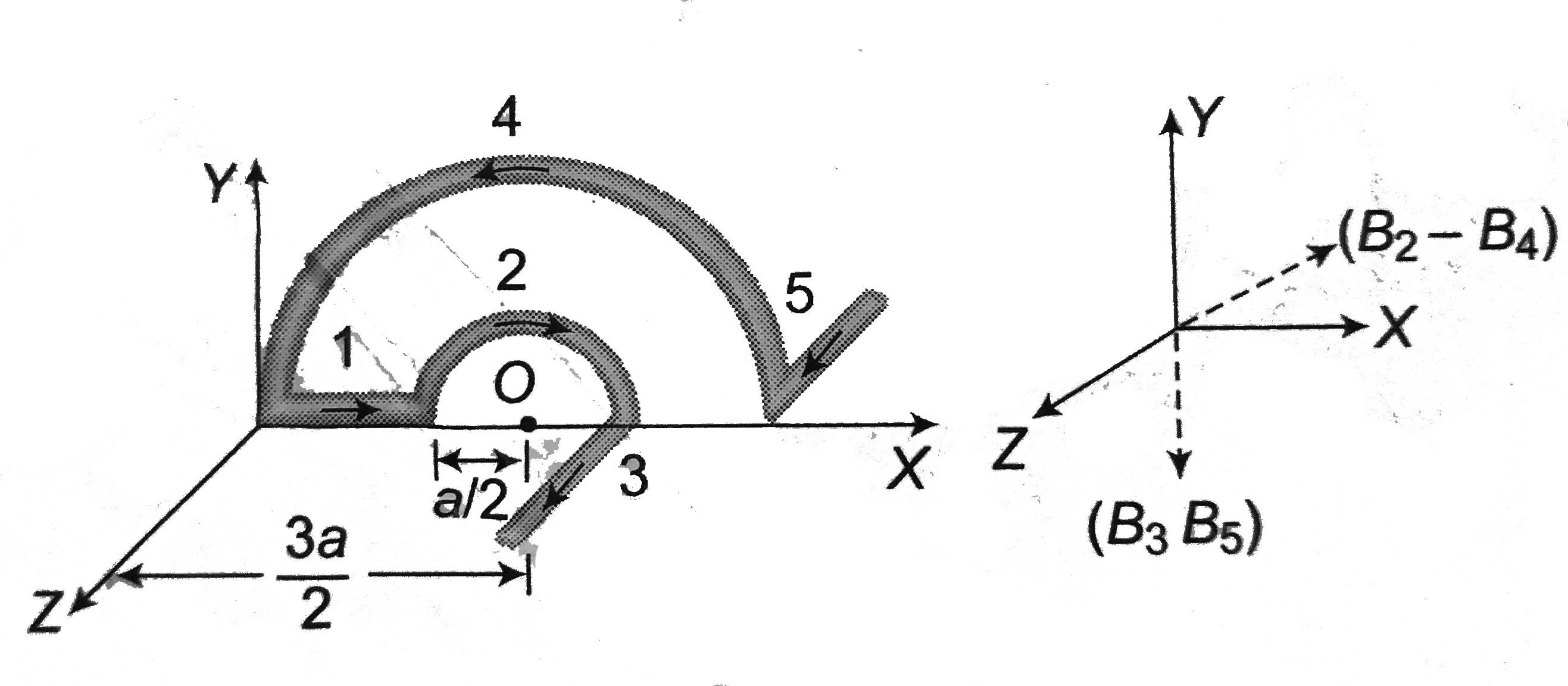
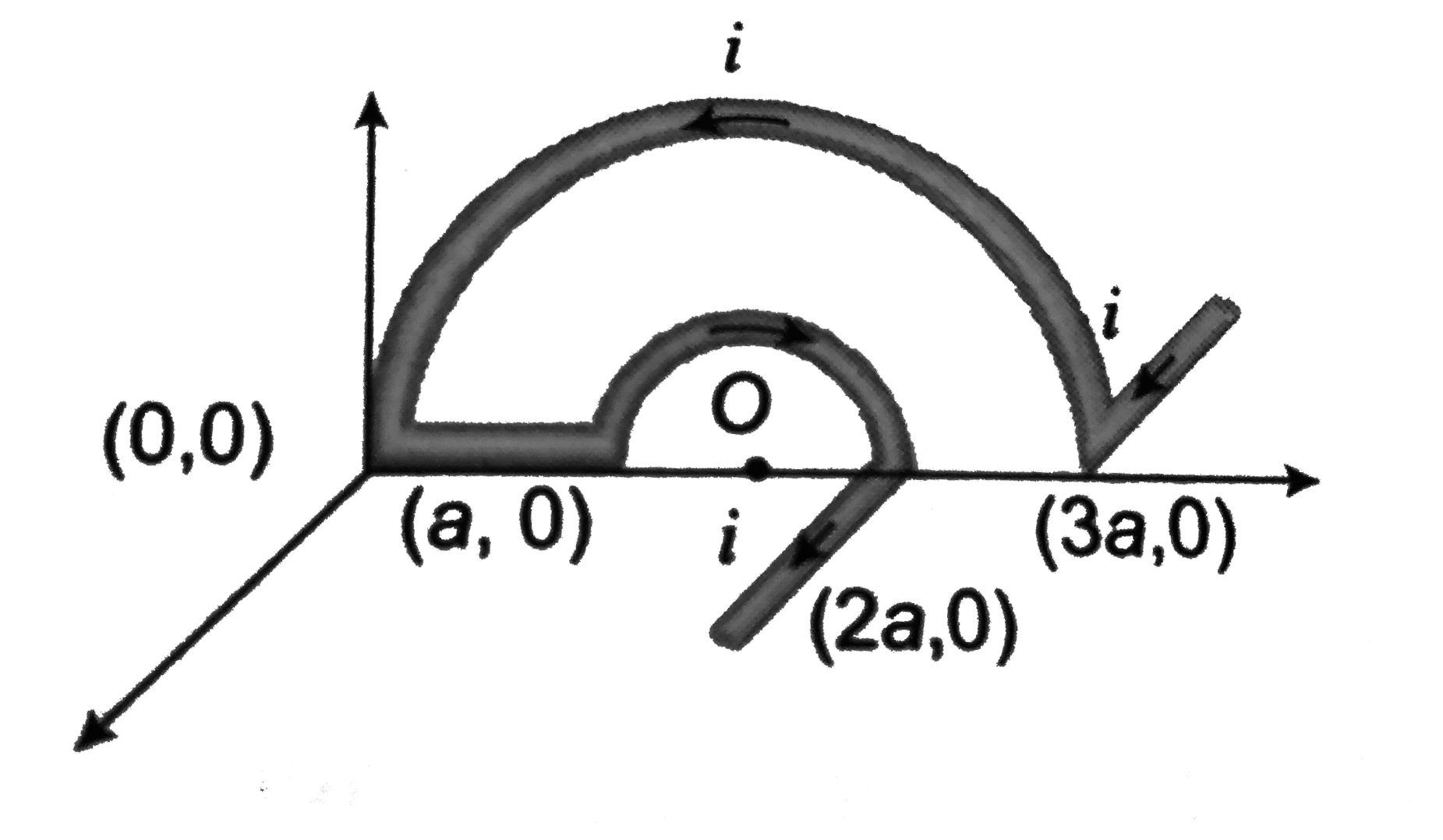
Magnetic field at O due to
Part(1): B1=0
Part(2): B2=μ04π.πi(a/2)⊗ (along-Z axis)
Part(3): B3=μ04π.πi(a/2)(⏐↓) (along Y axis)
Part(4): B_(4) =μ04π,.πi(3a/2)⊙ (along +Z axis)
Part(5)L B5=Bμ04π.i(3a/2)(⏐↓) (along −Y axis)
B2−B4=μ04π,πa(2−23)=μ0i3a⊗ (along −Z axis)
B3+B5=μ04π,1a(2+23)=8μ0i12πa(⏐↓) (along −Y axis)
Hence net magnetic field
Bnet=√(B2−B4)2+(B3+B5)2=μ0i3πa√π2+4
|
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Assertion- Reason
6 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
The magnetic field at O is
 AzeroB1C2D3
AzeroB1C2D3The magnetic field at O is
 Aμ0I2R√(14+1π2)Bμ0I2R√(12+1π2)Cμ0IR√(14+1π2)Dμ0IR√(14+1π)
Aμ0I2R√(14+1π2)Bμ0I2R√(12+1π2)Cμ0IR√(14+1π2)Dμ0IR√(14+1π)Find magnetic field at O.
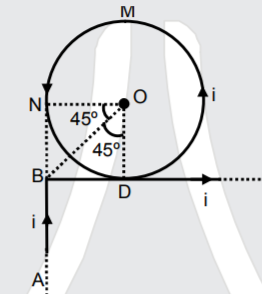 Aμ0i2πR[−1√2+π]Bμ0i2πR[π−1]Cμ0i2RDμ0i2πR[1√2+π]
Aμ0i2πR[−1√2+π]Bμ0i2πR[π−1]Cμ0i2RDμ0i2πR[1√2+π]
In the given figure the magnitude of magnetic field at O is ( all three wires are quarter circular ares )

View SolutionIn the given figure the magnetic induction at the point O is
View SolutionA current I flows through a long straight conductor which is bent into a circular loop of radius R in the middle as shown in the figure .
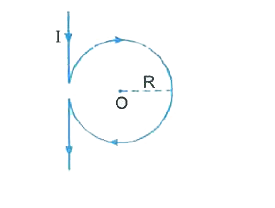
The magnitude of the net magnetic field at point O will be
View SolutionIn the given figure what is the magnetic field induction at point O?
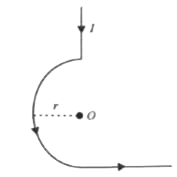
View SolutionIn the given figure what is the magnetic field induction at point O?

View Solution