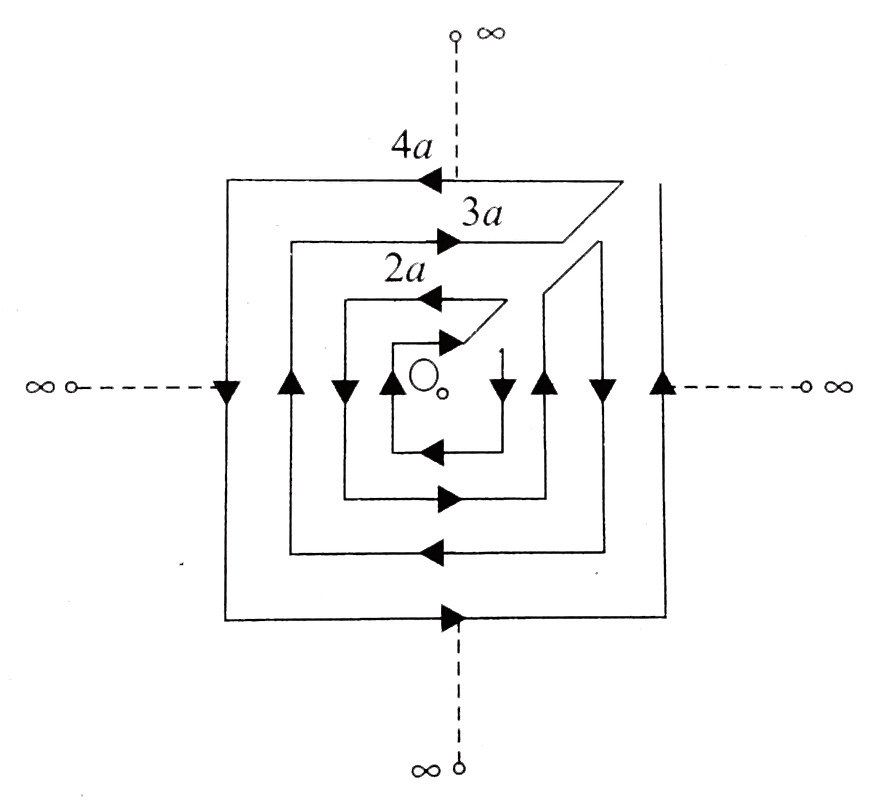
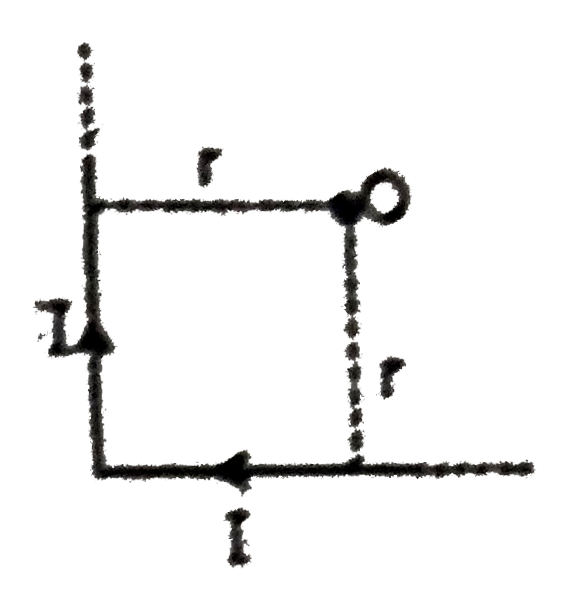
Determine the magnetic field at the centre of the current carrying wire arrangement shown in Fig. The arrangement extends to infinity. (The wires joining the successive squares are along the line passing through the centre).
A
μ0i√2πa
B
0
C
2√2μ0iπaln2
D
None of these
Video Solution
Text Solution
The correct Answer is:C
Magnetic field at centre due to a square of side a:
B=4[μ04πi(a/2)[sin45∘+sin45∘]]=2√2μ0iπa
For the case in fig.
Bnet=2√2μ0iπ[1a−12a+13a−14a+.....]
=2√2μ0iπa[1−12+13−14+.....]
=2√2μ0iπa(ln2)
|
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Section B - Assertion Reasoning
Explore 31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:AIPMTNEET Questions
Explore 47 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Magnetic Field Due To Circular Arc
Explore 69 Videos
- SEMICONDUCTOR ELECTRONICSBook:A2ZChapter:SEMICONDUCTOR ELECTRONICSExercise:EXERCISE
Explore 29 Videos
- WAVE OPTICSBook:A2ZChapter:WAVE OPTICSExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Knowledge Check
The magnetic field lines due to a straight wire carrying a current are
AstraightBcircularCparabolicDellipticalThe magnetic field at the centre O of the circular portion of radius 3cm carrying current 4 ampere in the wire is
 A(8π/3)×10−5TB(8π/3)×10−4TC2π×10−5TD2π×10−4T
A(8π/3)×10−5TB(8π/3)×10−4TC2π×10−5TD2π×10−4TThe magnetic field at the point O in the following current carrying square loop at the centre will be
 A12×10−5 TB4×10−5 TC4√2×10−5 TD2√2×10−5 T
A12×10−5 TB4×10−5 TC4√2×10−5 TD2√2×10−5 T
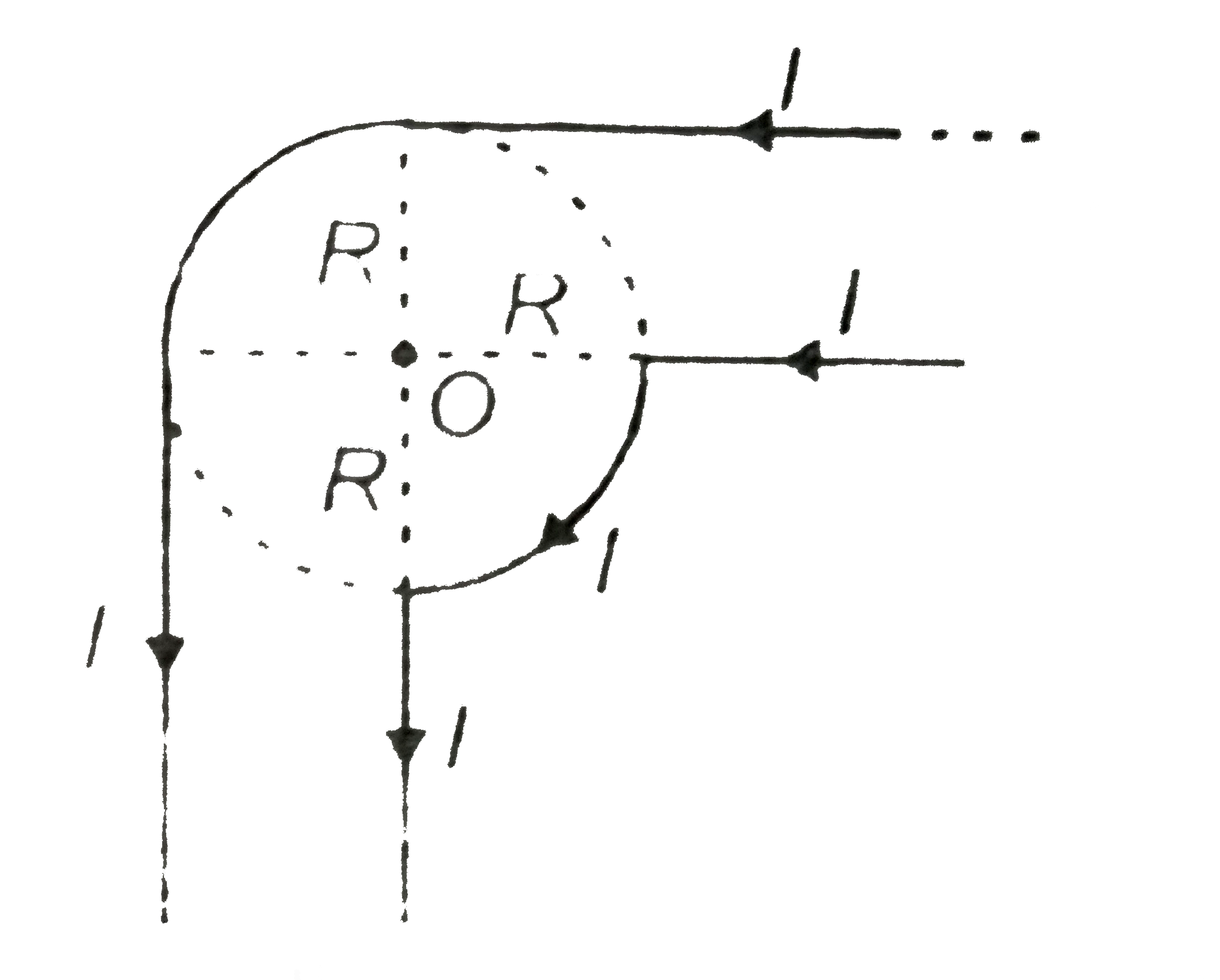
For the arrangement shown in Fig. determine the magnetic field at centre O.

View SolutionCalculate the force on a current carrying wire in a uniform magnetic field as shown in Fig. 1.59.

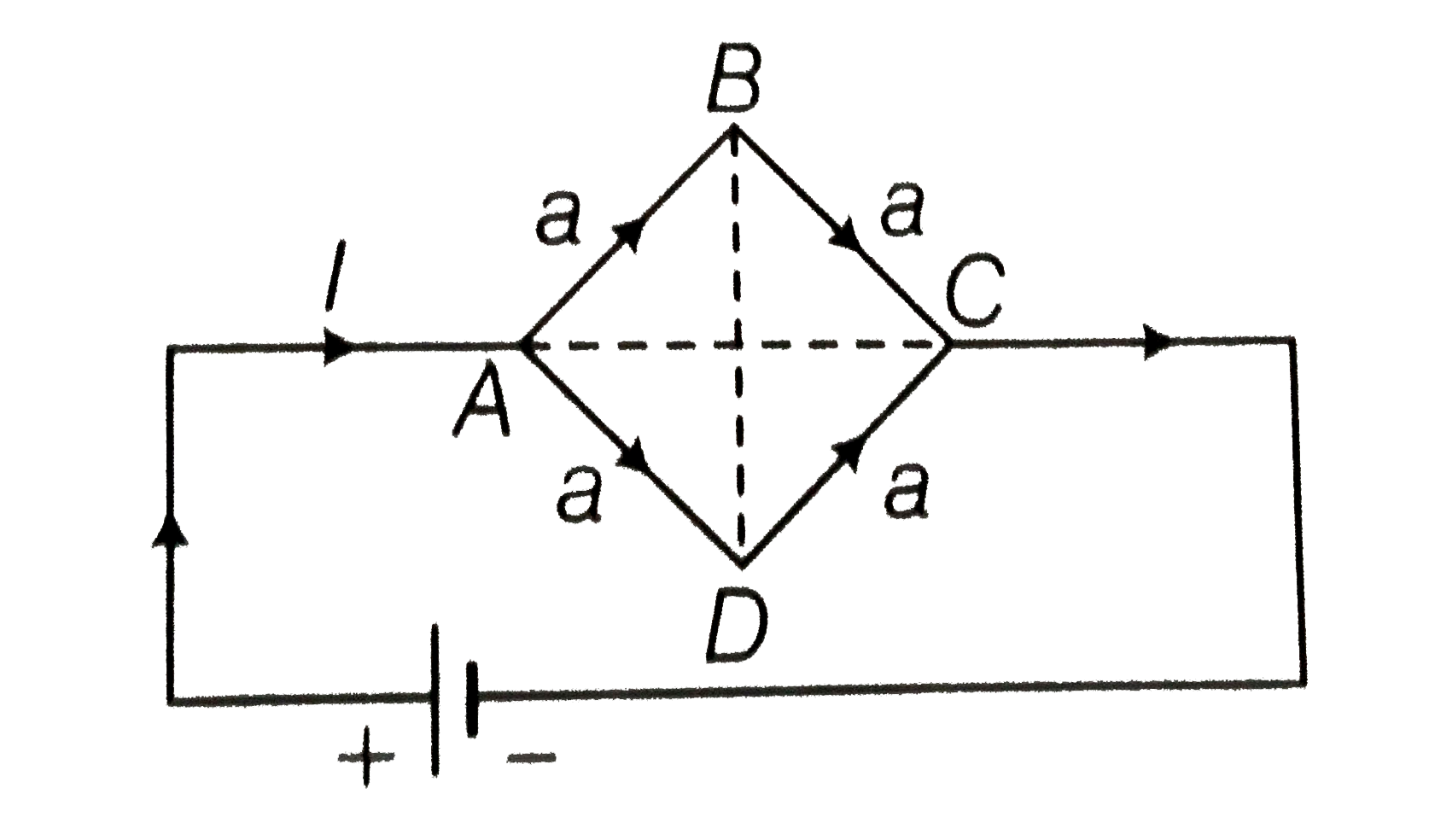
View SolutionMagnetic field induction at the centre O of a square loop of side a carrying current I as shown in figure.
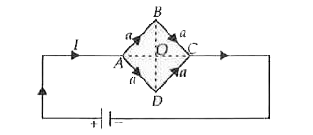
View SolutionMagnetic field induction at the centre of a square loop of side 'a' carrying current I as shown in figure is
View SolutionA current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
View Solution