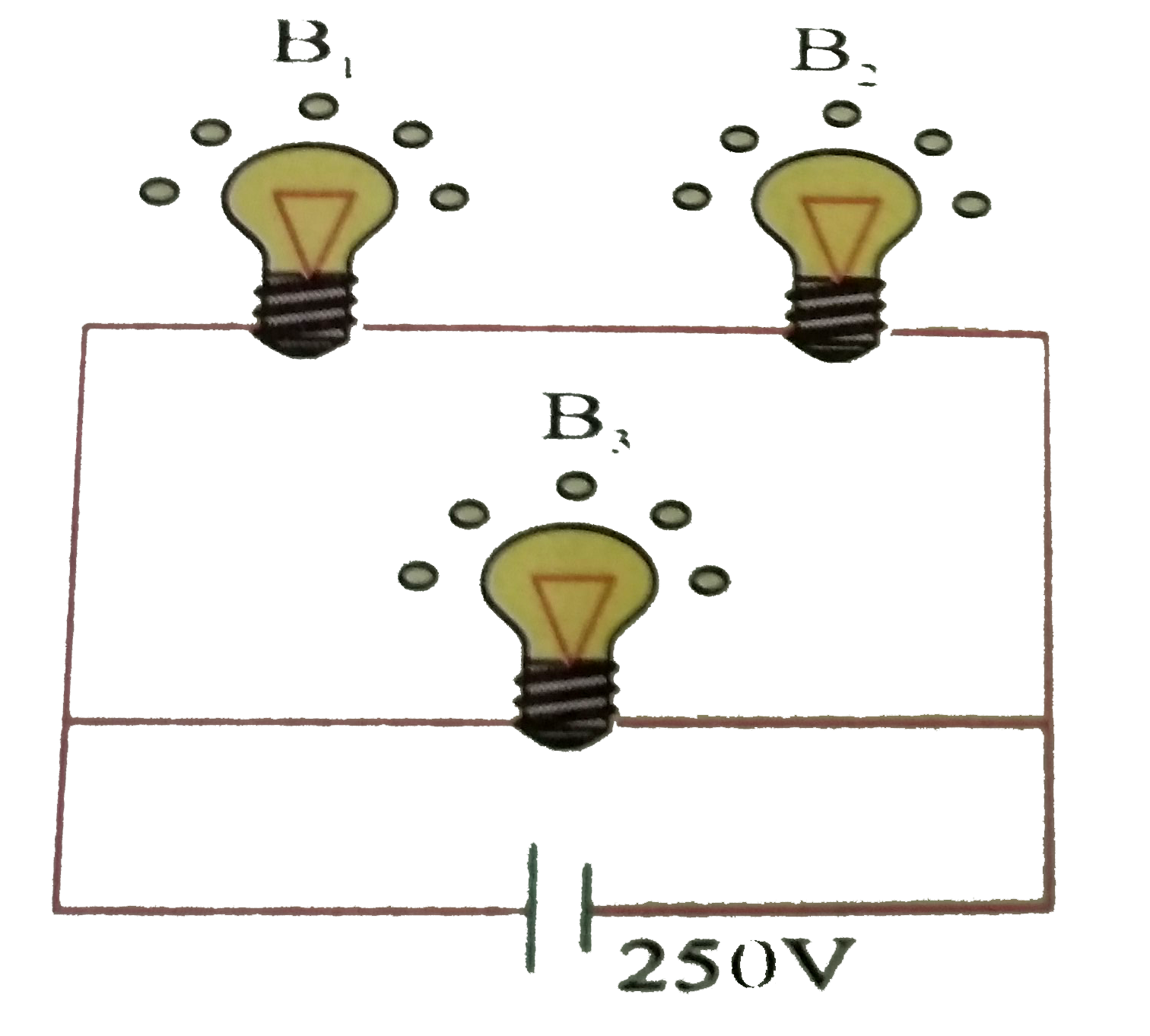
A 100 W bulb B1, and two 60 W bulb B2 and B3, are connected to a 250 V source, as shown in figure. Now W1,W2andW3 are the output powers of the bulbs B1,B2andB3, respectively. Then
W1>W2=W3
W1>W2>W3
W1<W2=W3
W1<W2<W3
The correct Answer is:D
(d) P=V2RsoR=V2P⇒R1=V2100 and R2=R3=V260
Now W1=(250)2(R1+R2)2.R1,W2=(250)2(R1+R2)2.R2
and W3=(250)2R3
W1:W2:W3=15:25:64 or W1<W2<W3
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:A2ZChapter:CURRENT ELECTRICITYExercise:Assertion- Reason
Explore 14 Videos
- ATOMIC PHYSICSBook:A2ZChapter:ATOMIC PHYSICSExercise:Section D - Chapter End Test
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
Knowledge Check
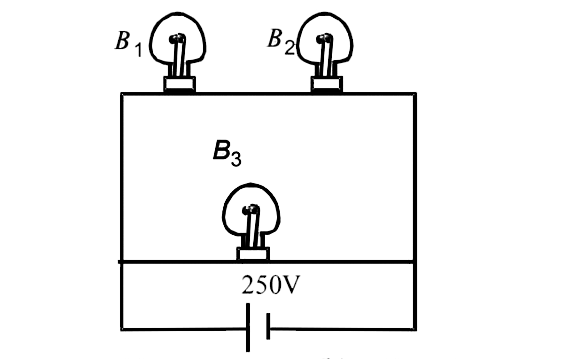
A 100 W bulb B1, and two 60 W bulb B2 and B3, are connected to a 250 V source, as shown in figure. Now W1,W2andW3 are the output powers of the bulbs B1,B2andB3, respectively. Then
 AW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3
AW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3Three bulbs of 40W,60Wand100W are connected in series with a 240V source.
AThe potential difference will be maximum across the 40W bulb .BThe current difference will be maximum in 100W bulb.CThe resistance of the 40W bulb is minimum.DThe current through the 60W bulb will be 0.1A.Bulb B1(100W−250W) and bulb B2(100W−200V) are connected across 250V. What is potential drop across B2 ?
 A200VB250VC98VD48V
A200VB250VC98VD48V
Three 60W,120V light bulbs are connected across a 120V power lines as shown in Fig. 7.26. Find (a) the voltage across each bulb and (b) the total power dissipated in the three bulbs.
View SolutionThree 60W,120V light bulbs are connected across a 120V power lines as shown in Fig. 7.26. Find (a) the voltage across each bulb and (b) the total power dissipated in the three bulbs.

View SolutionA 25 W , 220 V bulb and a 100 W , 220 V bulb are connected in parallel across a 440 V line
View SolutionTwo bulbs 100W,250V and 200W,250V are connected in parallel across a 500V line. Then-
View SolutionThree electric bulbs of 200 W, 200 W and 400 W are connected as shown in figure. The resultant power of the combination is
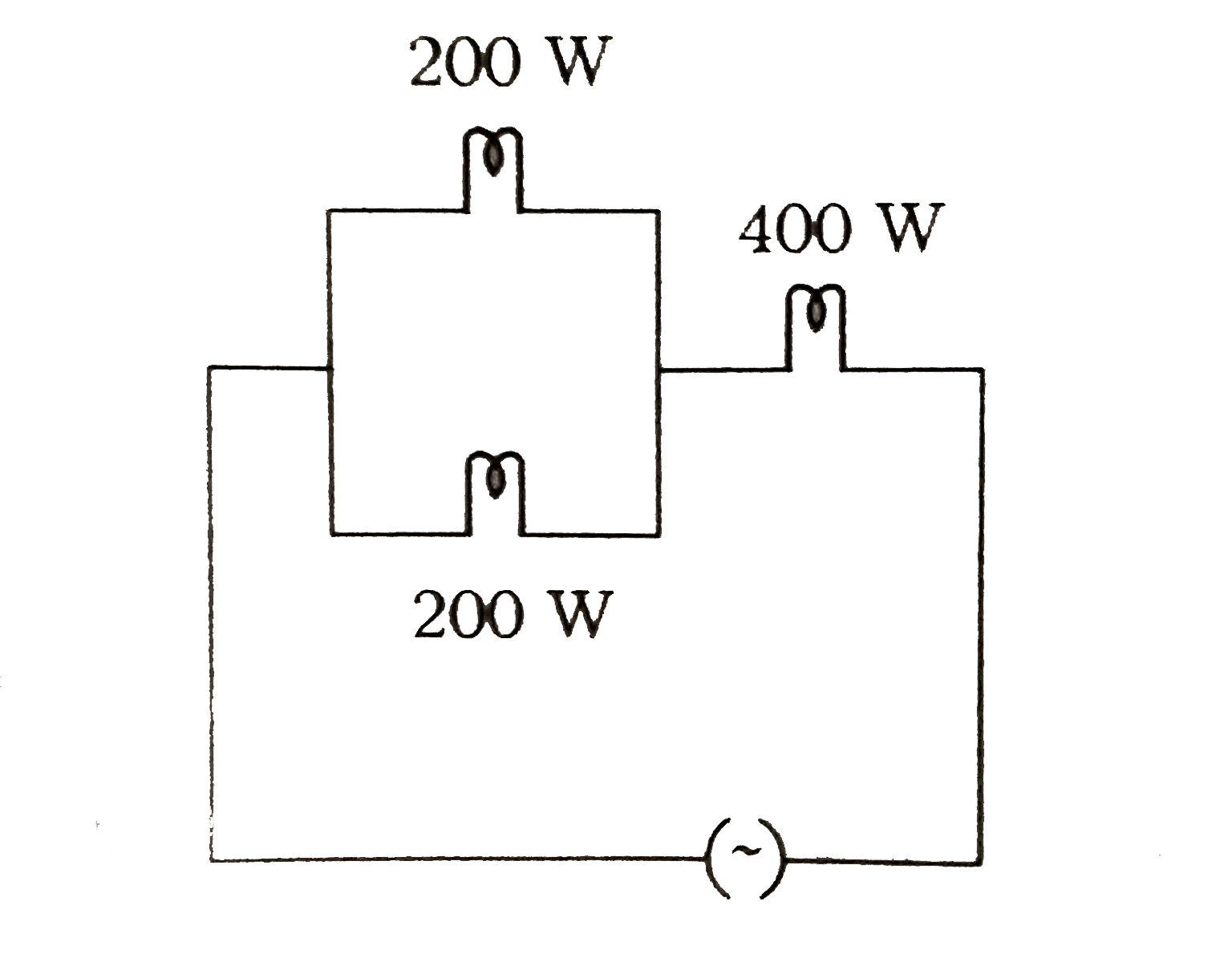
View Solution