Two ammeters, 1 and 2 have different internal resistances: r1 (known) and r2 (known). Each ammeter has scale such that the angular deviation of the needle for zero is proportional to the current passing through it. Initially, the ammeters are connected in series to a source of constant voltage. The deviations of the needles of the ammeter are θ1 and θ2, respecitively. The ammeters are then connected in parallel ot the same voltage source. This time, the deviations of the needles are θ'1 and θ'2 respectively. Find r2 in terms of r1,θ1,θ2,θ'1 and θ'2.
r1θ1θ'1θ2θ'2
r1θ2θ'1θ1θ'2
r1θ2θ'2θ1θ'1
r1θ2θ'2θ1θ'2
The correct Answer is:B
(b) In first case
i=k1,θ1,i=k2θ2k1,θ1=k2,θ2
In second case,
V1=V2⇒k1θ'1r1=k2θ'2r2
from (1) and (2), we get r2=r1θ2θ'1θ1θ'2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Potentiometer And Meter Bridge
45 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Heating Effect Of Current
40 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - R-C Circuits
17 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Three ammeters — 1, 2 and 3 have different internal resistances r1,r2andr3 respectively. Internal resistance r1 is known but r2andr3 are unknown. The angular deflection of pointer in each ammeter is proportional to the current. Initially, the three ammeters were connected in series to a voltage source (fig. a) and deflections for the three ammeters were θ1,θ2andθ3 respectively. The three ammeters were then connected in parallel to the same voltage source (fig. b). This time the deflections were observed to be θ'1,θ'2 and θ'3 respectively.
(a) Find r2andr3.
(b) If θ2=θ3 but θ'3>θ'2 then which one is larger r2orr3 ?
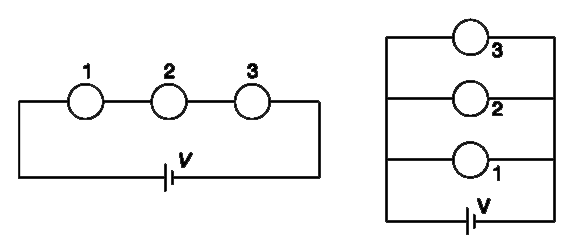
View SolutionWhy is ammeter connected in series and voltmeter in parallel in the circuit?
View Solution
Knowledge Check
When an ammeter is connected in parallel the resistance of the circuit is
AincreasedBdecreasedCis unchangedDnone of theseIf ammeter has zero resistance then –
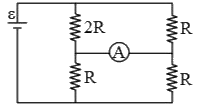 AReading of ammeter is ε6RBReading of ammeter is ε7RCReading of ammeter is ε8RDReading of ammeter is ε9R
AReading of ammeter is ε6RBReading of ammeter is ε7RCReading of ammeter is ε8RDReading of ammeter is ε9RAn ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
ABoth A and V increasesBBoth A and V decreasesCA decreases but V increasesDA increases but V decreases.
Which of the two is connected in series: ammeter or voltmeter?
View SolutionAn ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
View SolutionAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
View SolutionAn ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
View SolutionAn ammeter is connected in series with an unknown resistance and a voltmeter is connected across the terminals of the resistance . If the ammeter reads 1.2 A and the voltmeter reads 18 V the n value of the resistance is
View Solution
