Four point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
1q
Q=−q
Q=−1q
Q=q
The correct Answer is:B
To solve the problem, we need to find the relation between the charges Q and q such that the electric potential at the center of the square formed by the four charges is zero.
1. Identify the Charges and Their Positions:
- Let the charges be placed at the corners of a square with side length l.
- The charges are:
- Charge at (0, 0): −Q
- Charge at (0, l): −q
- Charge at (l, 0): 2q
- Charge at (l, l): 2Q
2. Calculate the Distance from Each Charge to the Center:
- The center of the square is at (l2,l2).
- The distance from each charge to the center (using the Pythagorean theorem) is:
r=√(l2−0)2+(l2−0)2=√l24+l24=√l22=l√2
3. Write the Expression for Electric Potential at the Center:
- The electric potential V at a point due to a point charge is given by:
V=kqr
- Therefore, the total potential Vtotal at the center due to all four charges is:
Vtotal=k⎛⎜⎝−Ql√2+−ql√2+2ql√2+2Ql√2⎞⎟⎠
- Simplifying this, we get:
Vtotal=k√2l(−Q−q+2q+2Q)
Vtotal=k√2l(Q+q)
4. Set the Total Potential to Zero:
- For the potential at the center to be zero:
Vtotal=0⇒Q+q=0
- This implies:
Q=−q
Conclusion:
The relation between Q and q for which the potential at the center of the square is zero is:
Q=−q
- Let the charges be placed at the corners of a square with side length l.
- The charges are:
- Charge at (0, 0): −Q
- Charge at (0, l): −q
- Charge at (l, 0): 2q
- Charge at (l, l): 2Q
- The center of the square is at (l2,l2).
- The distance from each charge to the center (using the Pythagorean theorem) is:
r=√(l2−0)2+(l2−0)2=√l24+l24=√l22=l√2
- The electric potential V at a point due to a point charge is given by:
V=kqr
- Therefore, the total potential Vtotal at the center due to all four charges is:
Vtotal=k⎛⎜⎝−Ql√2+−ql√2+2ql√2+2Ql√2⎞⎟⎠
- Simplifying this, we get:
Vtotal=k√2l(−Q−q+2q+2Q)
Vtotal=k√2l(Q+q)
- For the potential at the center to be zero:
Vtotal=0⇒Q+q=0
- This implies:
Q=−q
The relation between Q and q for which the potential at the center of the square is zero is:
Q=−q
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:AIIMS Questions
Explore 20 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Assertion Reason
Explore 8 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section B - Assertion Reasoning
Explore 17 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section D - Chapter End Test
Explore 29 Videos
- ELECTROMAGNETIC INDUCTIONBook:A2ZChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
Four point charges q1,q2,q3 and q4 are placed at the corners of the squares of side a,as shown in figure.Calculate the potential at the centre of the square.
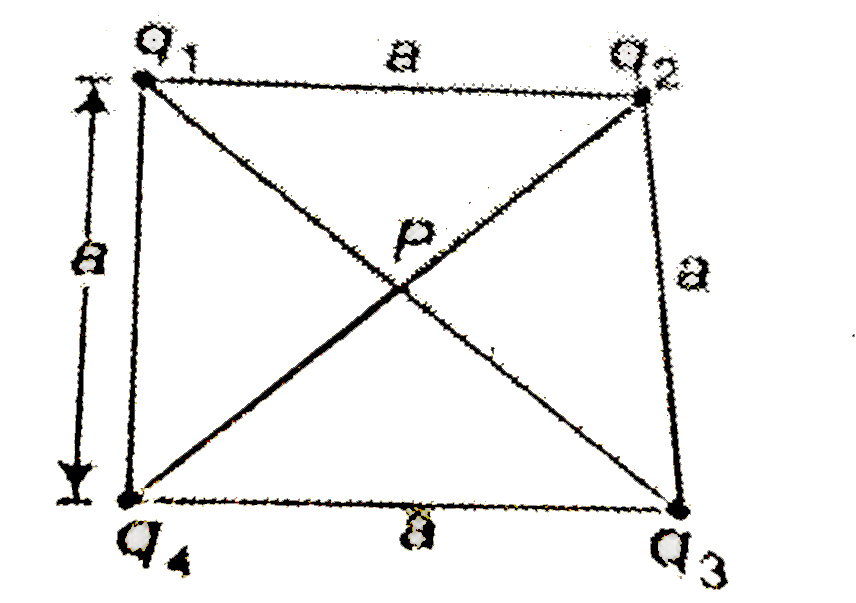
(Given, q1=1×10−8C,q2=−2×10−8C,q3=3×10−8C,q4=2×10−8C and a=1m)
View SolutionTwo point charges +Q each are placed at adjacent corners of a square. Other two point charges -Q each are placed at the remaining two corners of the same square . The side of the square is l. Find electric field intensity at the centre of the square.
View Solution
Knowledge Check
Four point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
AQ=−qBQ=1qCQ=qDQ=1qFour charges Q-Q, Q-Q are placed at the corners of a square as shown . The potential is zero at points
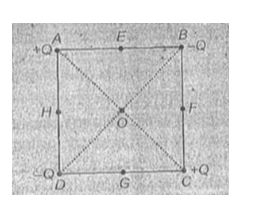 AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO only
AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO onlyCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
 AABBCBCBDDAC
AABBCBCBDDAC
Four charges +q,+2q,+3q and +4q are placed at the four corners ABCD of a square of side a. Calculate the field and potential at the centre of the square.
View SolutionFour charge Q,q,Q and q are kept at the four corners of a square as shown below. What is the relation between Q and q, so that the net force on a charge q is zero ?

View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
potential energy of this system .
View SolutionFour point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the Potential energy of this system.
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge Q
View Solution