Three equal charges Q are placed at the three vertices of an equilateral triangle. What should be the va,ue of a charge, that when placed at the centroid, reduces the interaction energy of the system to zero ?
−Q2
−Q3
−Q2√3
−Q√3
The correct Answer is:D
To solve the problem, we need to determine the value of a charge q that, when placed at the centroid of an equilateral triangle with three equal charges Q at its vertices, will reduce the interaction energy of the system to zero.
1. Understanding the Setup:
- We have three equal charges Q located at the vertices of an equilateral triangle.
- The centroid of the triangle is the point where we will place the charge q.
2. Distance from Centroid to Vertex:
- For an equilateral triangle with side length A, the distance from the centroid to each vertex is given by:
L=A√3
3. Calculating the Interaction Energy:
- The interaction energy U of the system with the three charges Q at the vertices can be calculated using the formula for potential energy between point charges:
U=k(Q⋅QA+Q⋅QA+Q⋅QA)=3kQ2A
- Here, k is Coulomb's constant.
4. Energy Contribution from Charge q:
- When we place charge q at the centroid, it will interact with each of the three charges Q. The potential energy due to these interactions is:
Uq=3⋅kQ⋅qL=3⋅kQ⋅qA√3=3⋅kQ⋅q⋅√3A
5. Setting Total Energy to Zero:
- To reduce the total interaction energy of the system to zero, we need:
U+Uq=0
- Substituting the expressions we found:
3kQ2A+3⋅kQ⋅q⋅√3A=0
- Dividing through by 3k/A (assuming k≠0 and A≠0):
Q+q⋅√3=0
6. Solving for Charge q:
- Rearranging gives:
q⋅√3=−Q
- Therefore, the value of charge q is:
q=−Q√3
Final Answer:
The charge q that should be placed at the centroid to reduce the interaction energy of the system to zero is:
q=−Q√3
- We have three equal charges Q located at the vertices of an equilateral triangle.
- The centroid of the triangle is the point where we will place the charge q.
- For an equilateral triangle with side length A, the distance from the centroid to each vertex is given by:
L=A√3
- The interaction energy U of the system with the three charges Q at the vertices can be calculated using the formula for potential energy between point charges:
U=k(Q⋅QA+Q⋅QA+Q⋅QA)=3kQ2A
- Here, k is Coulomb's constant.
- When we place charge q at the centroid, it will interact with each of the three charges Q. The potential energy due to these interactions is:
Uq=3⋅kQ⋅qL=3⋅kQ⋅qA√3=3⋅kQ⋅q⋅√3A
- To reduce the total interaction energy of the system to zero, we need:
U+Uq=0
- Substituting the expressions we found:
3kQ2A+3⋅kQ⋅q⋅√3A=0
- Dividing through by 3k/A (assuming k≠0 and A≠0):
Q+q⋅√3=0
- Rearranging gives:
q⋅√3=−Q
- Therefore, the value of charge q is:
q=−Q√3
The charge q that should be placed at the centroid to reduce the interaction energy of the system to zero is:
q=−Q√3
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section B - Assertion Reasoning
17 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - AIPMTNEET Questions
38 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor Circuits
52 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Three points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
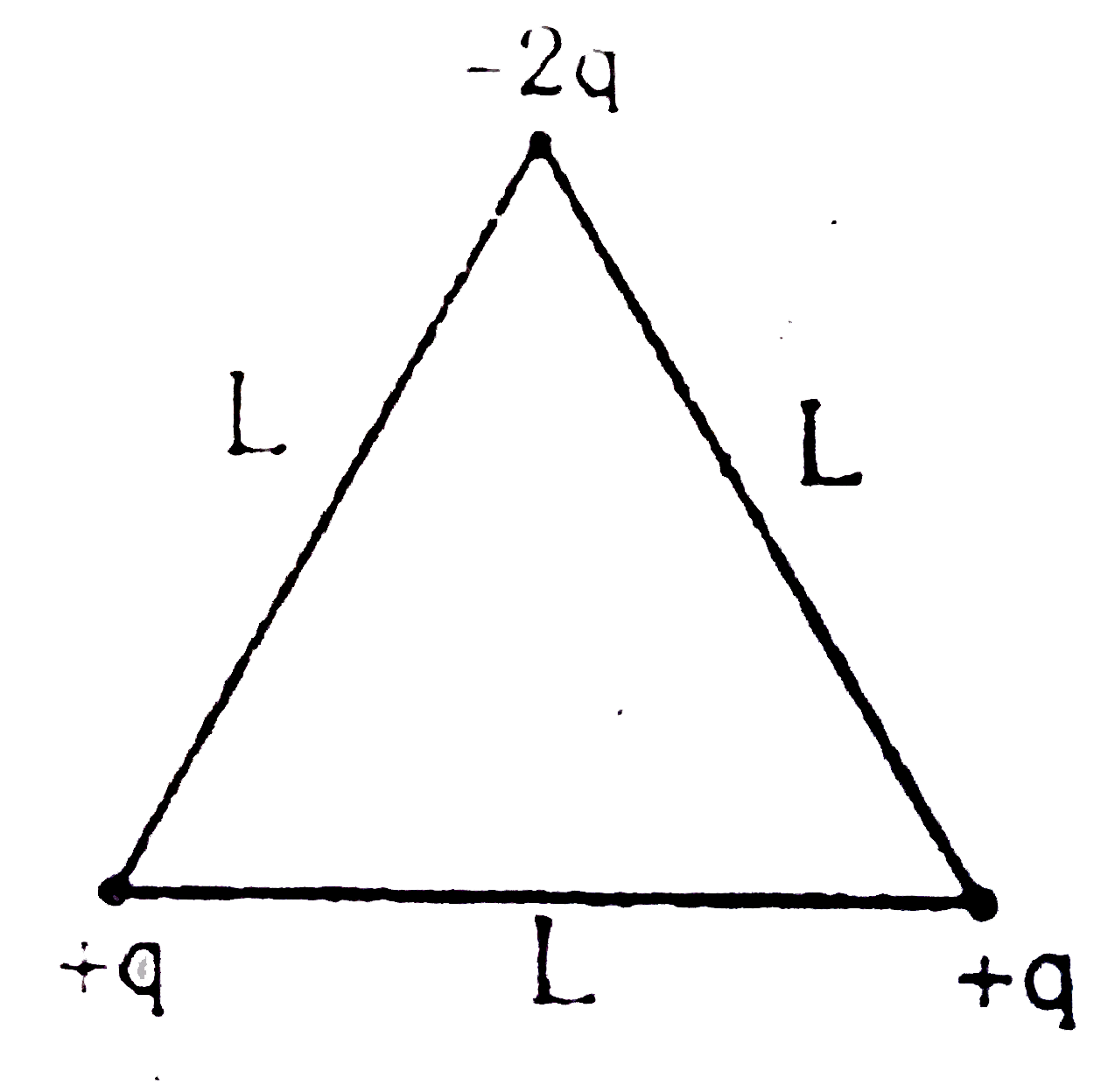
View SolutionThree point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that electric potential energy of the system is zero.
View Solution
Knowledge Check
Three charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
A√3qaB√3qa2C√2qaDqa2Three equal charges Q are placed at the three corners of an equilateral triangle of side length a. Work done in shifting a charge q from infinity to the centroid of the triangle is
A3Qq4π∈0aB3Qq4π∈0√3aC3√3Qq4π∈0aD√3Qq4π∈03aThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree charges q1,q2,q3 each equal to q placed at the vertices of an equilateral triangle of side l . What will be the force on a charge Q placed at the centroid of triangle ?
View SolutionThree identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
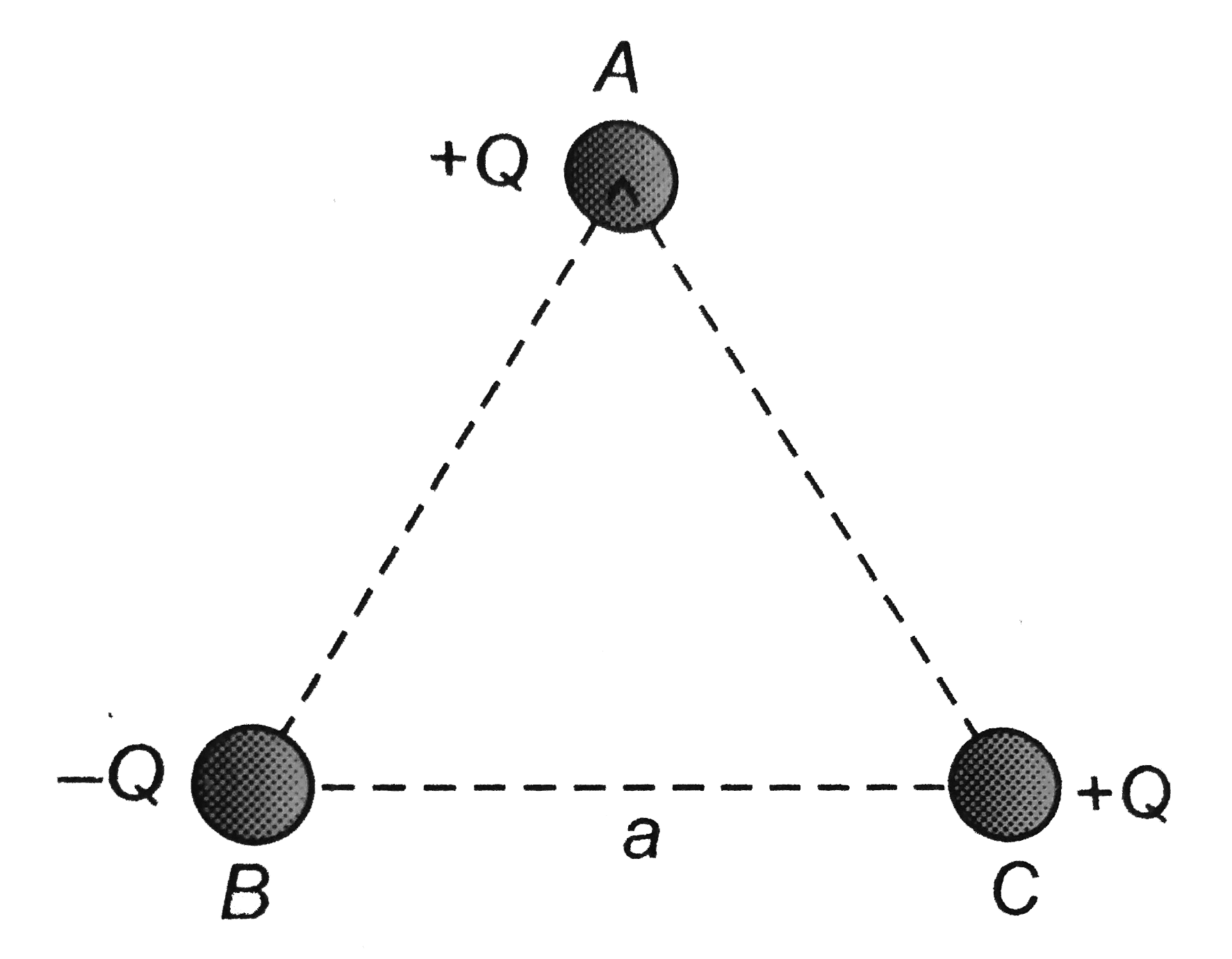
View SolutionThree charges are placed at the vertices of an equilateral trianlge of side a as shown in the following figure. The force experienced by the charge placed at the vertex A in a direction normal to BC is
View Solution