A capacitor of capacity C(1) is charged to the potential of V(0). On d

A capacitor of capacity $C_{1}$ is charged to the potential of $V_{0}$ . On disconnecting with the battery, it is connected with a capacitor of capacity $C_{2}$ as shown in the adjoining figure. The ratio of energies before and after the connection of switch S will be

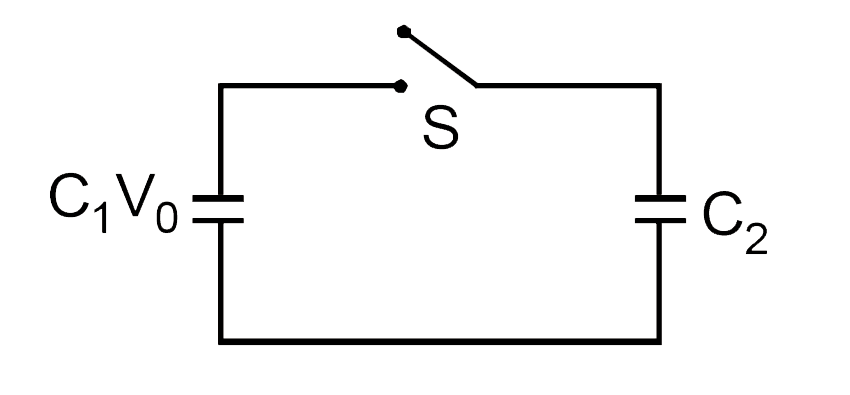A $(C_{1} + C_{2}) / C_{1}$
B $C_{1} / (C_{1} + C_{2})$
C $C_{1} C_{2}$
D $C_{1} / C_{2}$
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then
AEnergy stored in capacitor and inductor will be equal at time $t = \frac{π}{2} \sqrt{L} C$
BPotential difference across inductor will be $\frac{V}{2}$ at time $t = \frac{π}{3} \sqrt{L} C$
CThe rate of increase of energy in magnetic field will be maximum at $\frac{π}{4} \sqrt{L} C$
DWhen the potentail difference across the capacitor $\sqrt{(\frac{3 C}{L})}$
A capacitor C is charged to a potential V by a battery. It is then disconnected from the battery and again connected with its polarity reversed to the battery
AThe work done by the battery is $C V^{2}$
BThe total charge the passes through battery is 2 CV
CThe initial and final energy of the capacitor is same
DThe work done by the battery is $2 C V^{2}$

A capacitor of capacity $C_{1}$ is charged to the potential of $V_{0}$ . On disconnecting with the battery, it is connected with a capacity $C_{2}$ as shown in the adjoining figure. The ratio of energies before and after the connection of switch $S$ will be