0.2F capacitor is charged to 600V by a battery. On removing the battery it is connected with another parallel plate condenser of 1F. The potential decreases to
100 volts
120 volts
300 volts
600 volts
The correct Answer is:A
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the initial charge on the capacitor
The initial charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
where:
- C=0.2F (capacitance of the first capacitor)
- V=600V (voltage across the first capacitor)
Substituting the values:
Q=0.2F⋅600V=120C
Step 2: Understand the connection of the second capacitor
When the charged capacitor is connected to the second capacitor (1 F), they are in parallel. In parallel, the voltage across both capacitors will be the same after they are connected.
Step 3: Set up the equations for charge conservation
Let Q1 be the charge on the 0.2 F capacitor and Q2 be the charge on the 1 F capacitor after they are connected. The total charge before connecting the capacitors must equal the total charge after they are connected:
Q1+Q2=120C
Step 4: Relate the charges to the voltages
The voltage across each capacitor after connection will be the same, denoted as Vf. Therefore, we can express the charges as:
Q1=C1⋅Vf=0.2⋅Vf
Q2=C2⋅Vf=1⋅Vf
Step 5: Substitute into the charge conservation equation
Substituting these expressions into the charge conservation equation:
0.2Vf+1Vf=120
1.2Vf=120
Step 6: Solve for the final voltage Vf
Now, solve for Vf:
Vf=1201.2=100V
Conclusion
The potential across the capacitors after connecting them will decrease to:
100V
---
The initial charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
where:
- C=0.2F (capacitance of the first capacitor)
- V=600V (voltage across the first capacitor)
Q=0.2F⋅600V=120C
When the charged capacitor is connected to the second capacitor (1 F), they are in parallel. In parallel, the voltage across both capacitors will be the same after they are connected.
Let Q1 be the charge on the 0.2 F capacitor and Q2 be the charge on the 1 F capacitor after they are connected. The total charge before connecting the capacitors must equal the total charge after they are connected:
Q1+Q2=120C
The voltage across each capacitor after connection will be the same, denoted as Vf. Therefore, we can express the charges as:
Q1=C1⋅Vf=0.2⋅Vf
Q2=C2⋅Vf=1⋅Vf
Substituting these expressions into the charge conservation equation:
0.2Vf+1Vf=120
1.2Vf=120
Now, solve for Vf:
Vf=1201.2=100V
The potential across the capacitors after connecting them will decrease to:
100V
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor Circuits
52 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Problems Based On Mixed Concepts
44 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor With Dielectric
32 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A 2μF condenser is charged upto 200 volt and then battery is removed. On combining this with another uncharged condenser in parallel, the potential difference is found to be 40 volt. Find the capacity of second condenser (in μF)
View SolutionA μF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
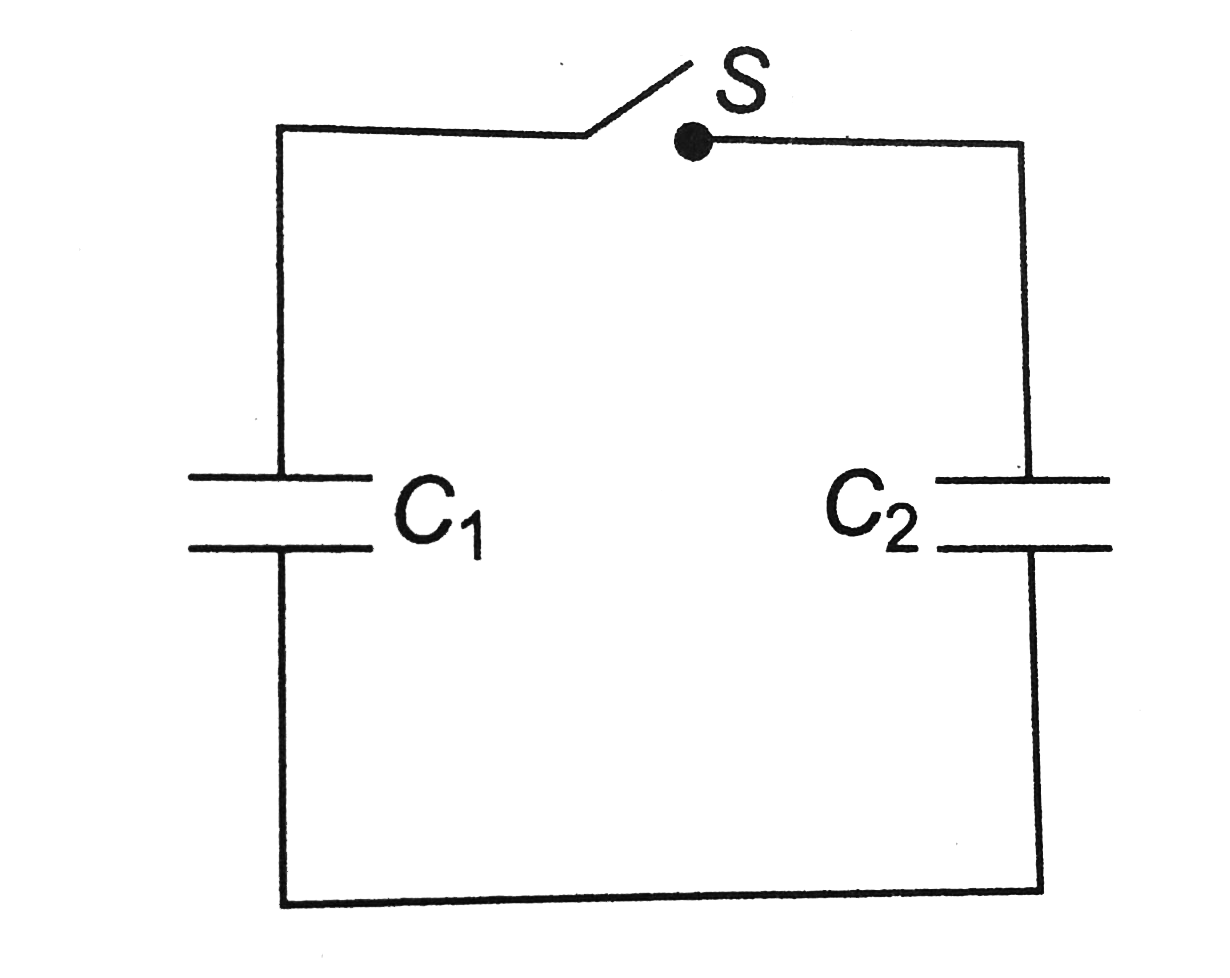
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View Solution
Knowledge Check
STATEMENT-1: A parallel plate capacitor is charged by a battery. The battery is then disconnected. If the distance the plates is increased, the enegry strored in the capacitor will decrease.
STATEMENT-2: Work has to be done to increase the separation between the plates of a charged capacitor.AStatement -1 si Ture, Statement -2 is True, Statement -2 is a correct explanation for Statement -1.BStatement-1 is True, Statement-2 is True, Statement-2 is Not a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.A 2μF condenser is charged upto 200 V and then battery is removed. On combining this with another uncharged condenser in parallel, the potential differences between two plates are found to be 40 V. The capacity of second condenser is
A2μFB4μFC8μFD16μFA capacitor C is charged to a potential V by a battery. It is then disconnected from the battery and again connected with its polarity reversed to the battery
AThe work done by the battery is CV2BThe total charge the passes through battery is 2 CVCThe initial and final energy of the capacitor is sameDThe work done by the battery is 2CV2
A parallel plate capacitor is charged by connecting it to a battery. The battery is disconnected and the plates of the capacitor are pulled apart to make the separation between the plates twice. Again the capacitor is connected to the battery (with same polarity) then the potential difference between the plates increases when the plates are pulled apart (yes or not)
View SolutionThe plates of a parallel plate capacitor are charged by a battery and the battery is disconnected after the charging. Now, the plates are placed as shown in the figure. Then (plates are not parallel to each other).
 .
.
View SolutionA capacitor is fully changed with a battery. Then the battery is removed and a coil is connected with the capacitor in parallel, current varies as
View SolutionThe plates of a parallel plate capacitor are charged up to 100v. Now, after removing the battery, a 2mm thick plate is inserted between the plates Then, to maintain the same potential deffernce, the distance betweem the capacitor plates is increase by 1.6mm. The dielectric canstant of the plate is .
View SolutionA 80 pF capacitor is charged to 15 V by connecting it to a battery. How many electrons are transferred from one plate to another?
View Solution
