In a figure shown find the ratio of the linear charge densites λ1 (on semi-infinite straight wire) and λ2 (on semi-circular part) that is, λ1/λ2 so that the field at O is along y direction.
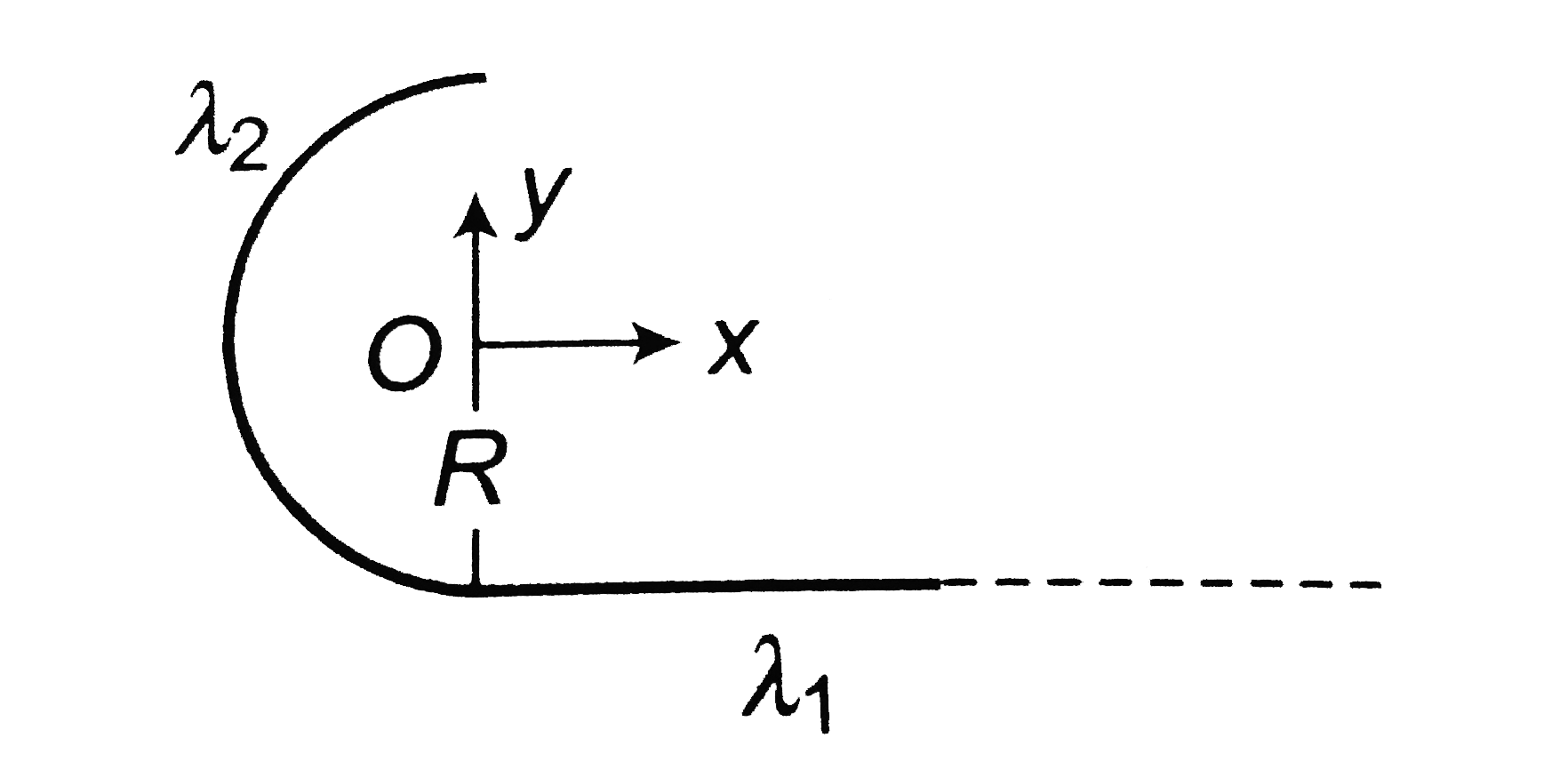
2
1.5
3
2.5
The correct Answer is:a
Electric field due to semicircular part:
E2=λ22πε0R
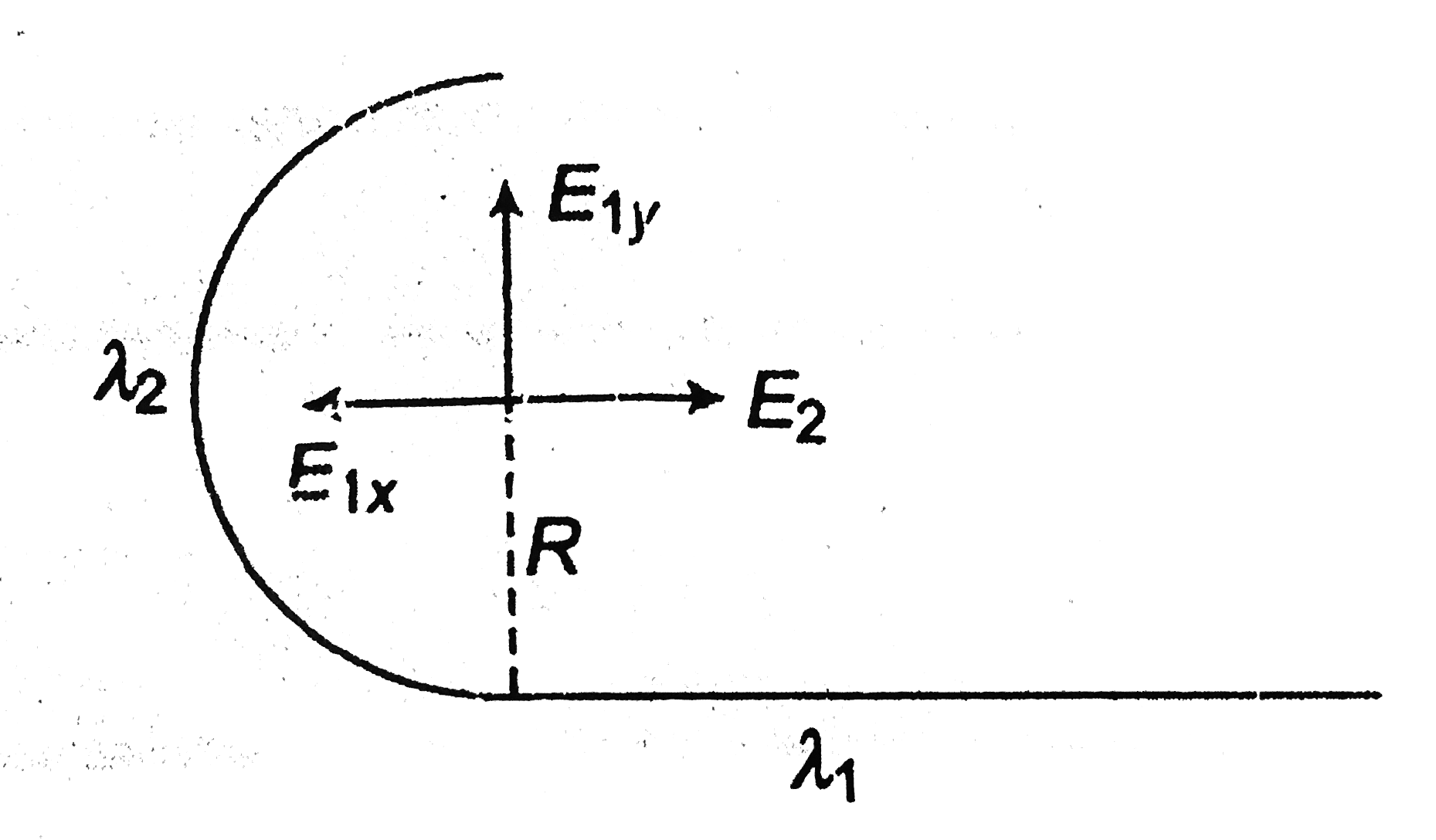
Electric field due to straight part:
E1x=E1y=λ14πε0R
For net field to be along y-axis:
E2=E1x⇒λ22πε0R=λ14πε0R⇒λ1λ2=2
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Assertion Reason
Explore 7 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Knowledge Check
If linear charge density of a wire as shown in the figure is λ
 Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the aboveThe linear charge density on upper half of semi-circular section of ring is λ and that at lower half is −λ. The direction of electric field at centre O of ring is :
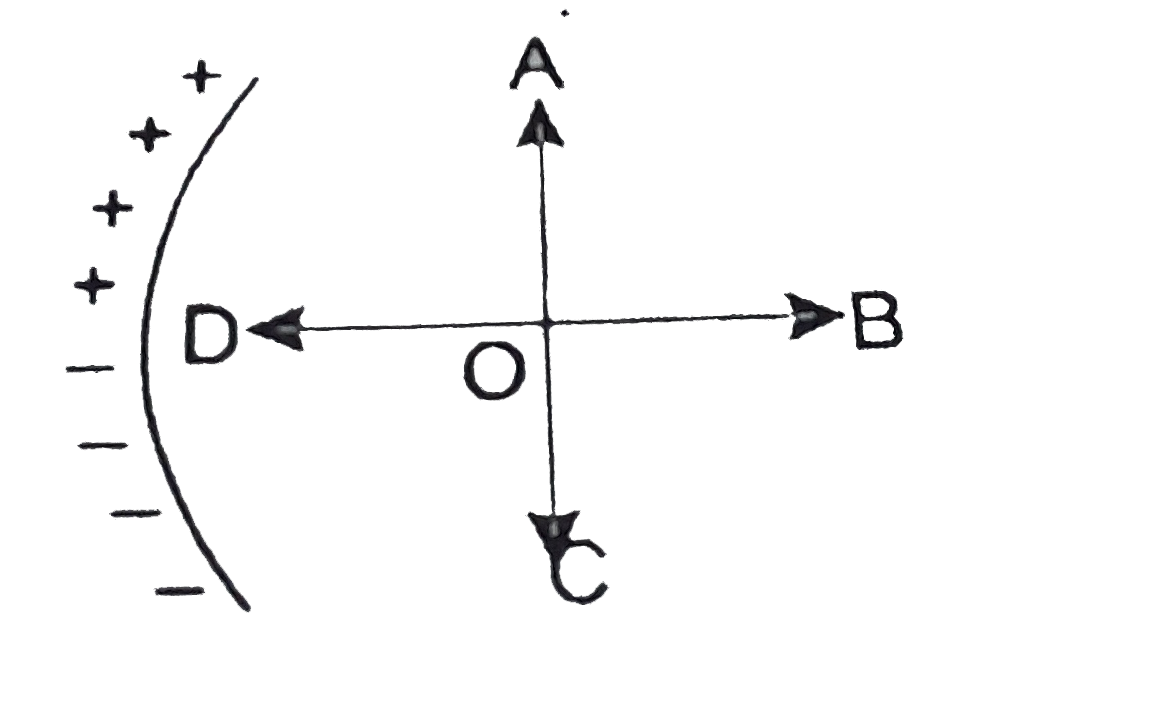 Aalong OABalong OBCalong OCDalong OD
Aalong OABalong OBCalong OCDalong ODFor balmer series wavelength of first line is λ1 and for brackett series wavelength of first line is λ2 then λ1λ2 is
A0.81B0.162C0.198D0.238
A proton with KE equal to that a photono (E = 100 keV). λ1 is the wavelength of proton and λ2 is the wavelength of photon. Then λ1λ)2 is proportional to:
View SolutionA circular wire of radius r has a uniform linear charge density λ=λ0cos2θ, The total charge on the wire is απλ0r2 Find α.
View SolutionFor balmer series wavelength of first line is λ1 and for brackett series wavelength of first line is λ2 then λ1λ2 is
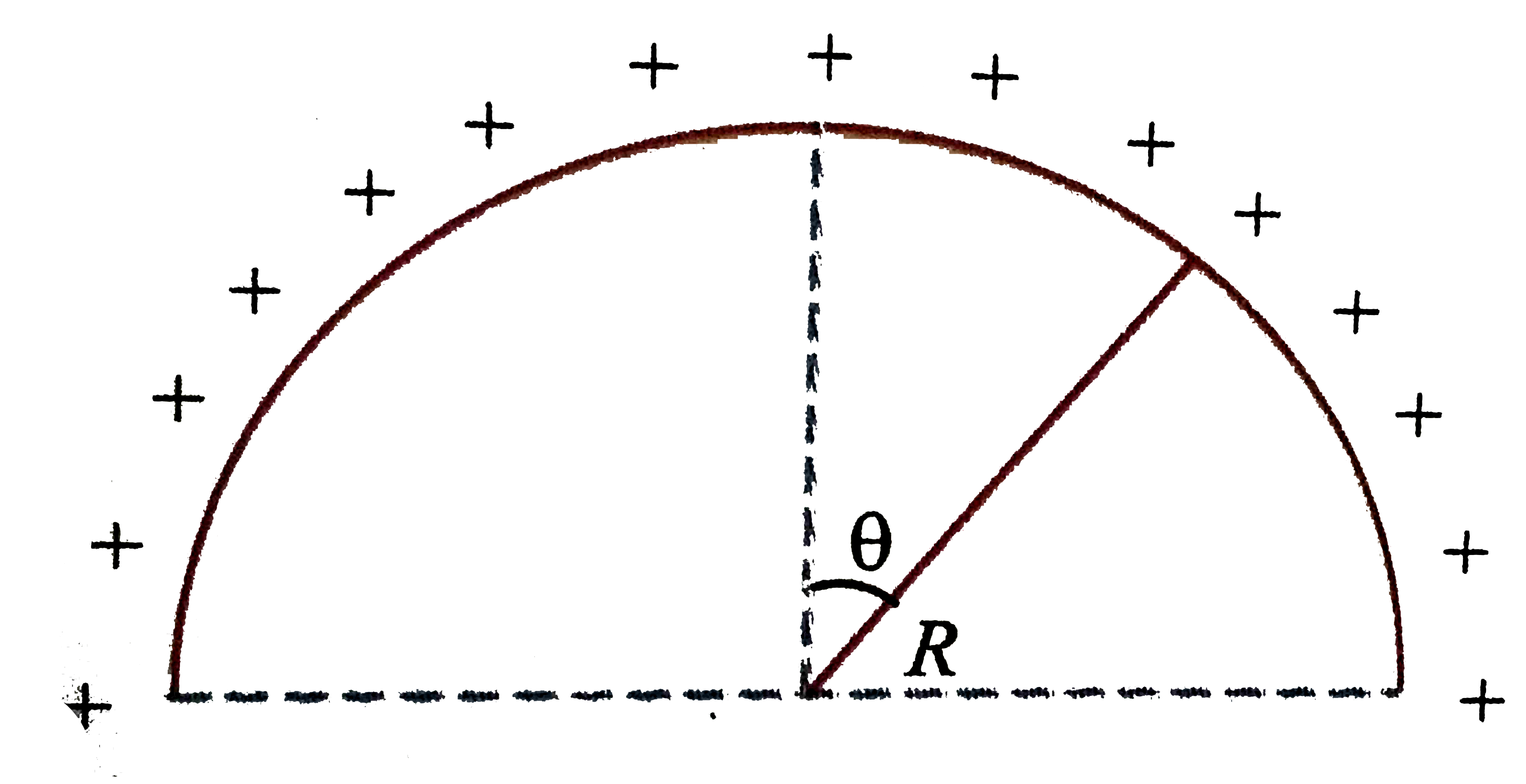
View SolutionThe linear charge density of a uniform semicircular wire varies with θ shown in the figure as λ=λ0cosθ if R is the radius of the loop ,of the charge on the wire is
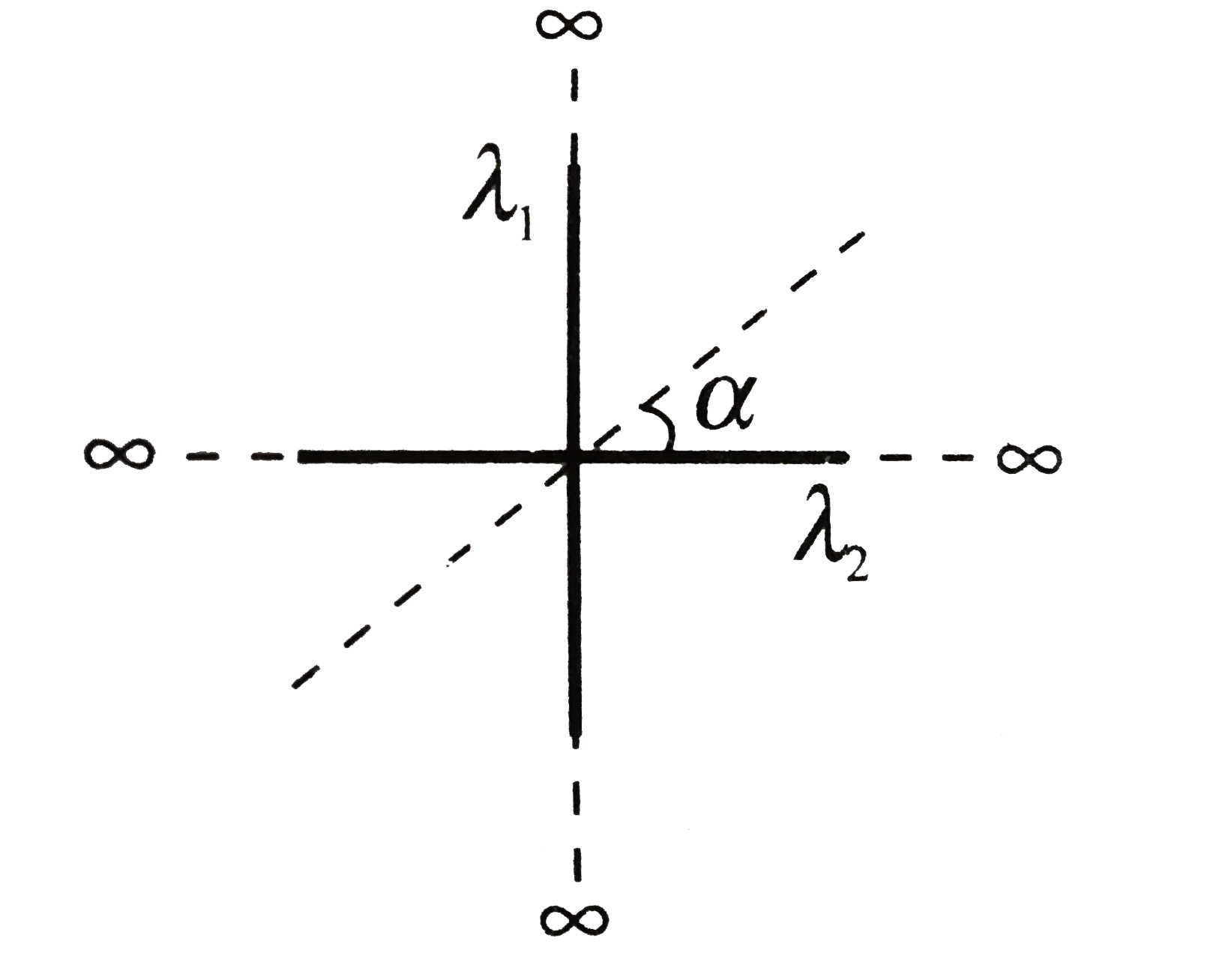
View SolutionTwo mutually perpendicular wire carry charge densities λ1andλ2. The electric lines of force makes angle α with second wire, then λ1/λ2 is
View Solution
