Two concentric coducting thin spherical shells A and B having radii rA and rB(rB>rA) are charged to QA and −QB(|QB|>|QA|). The electrical field along a line passing through the centre is
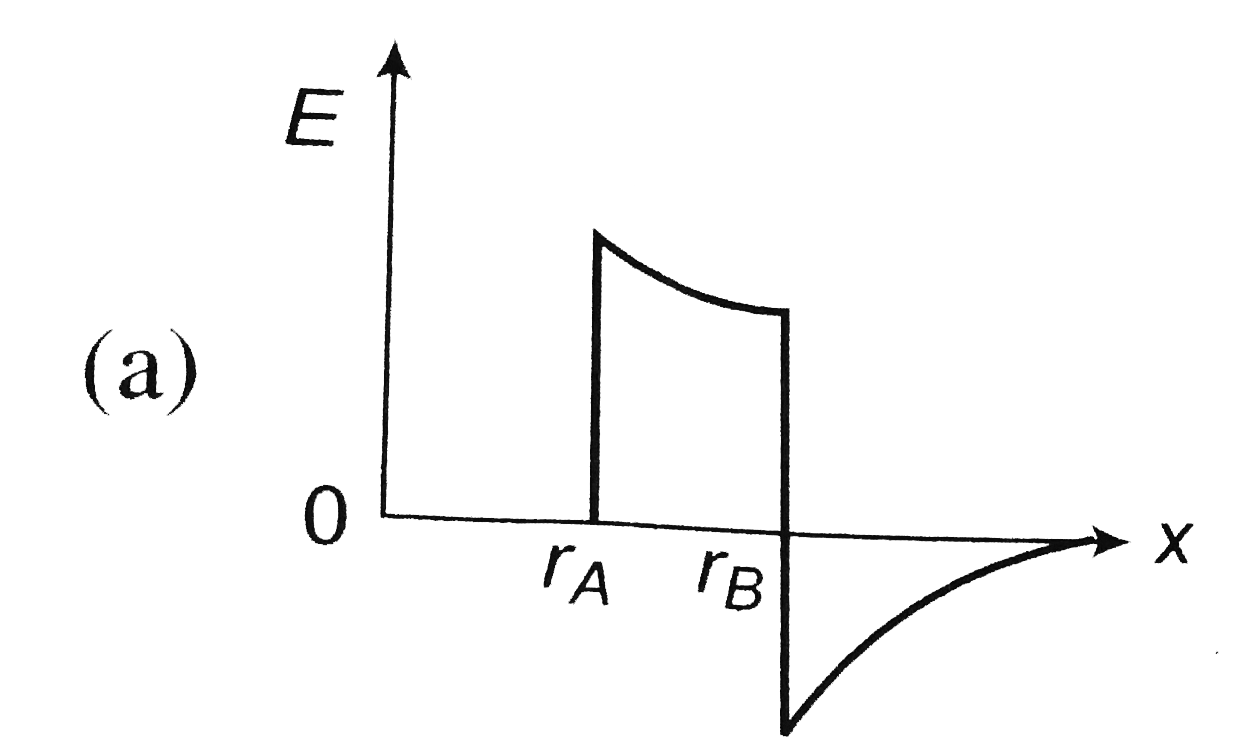

The correct Answer is:a
The electric field inside the shell A is zero
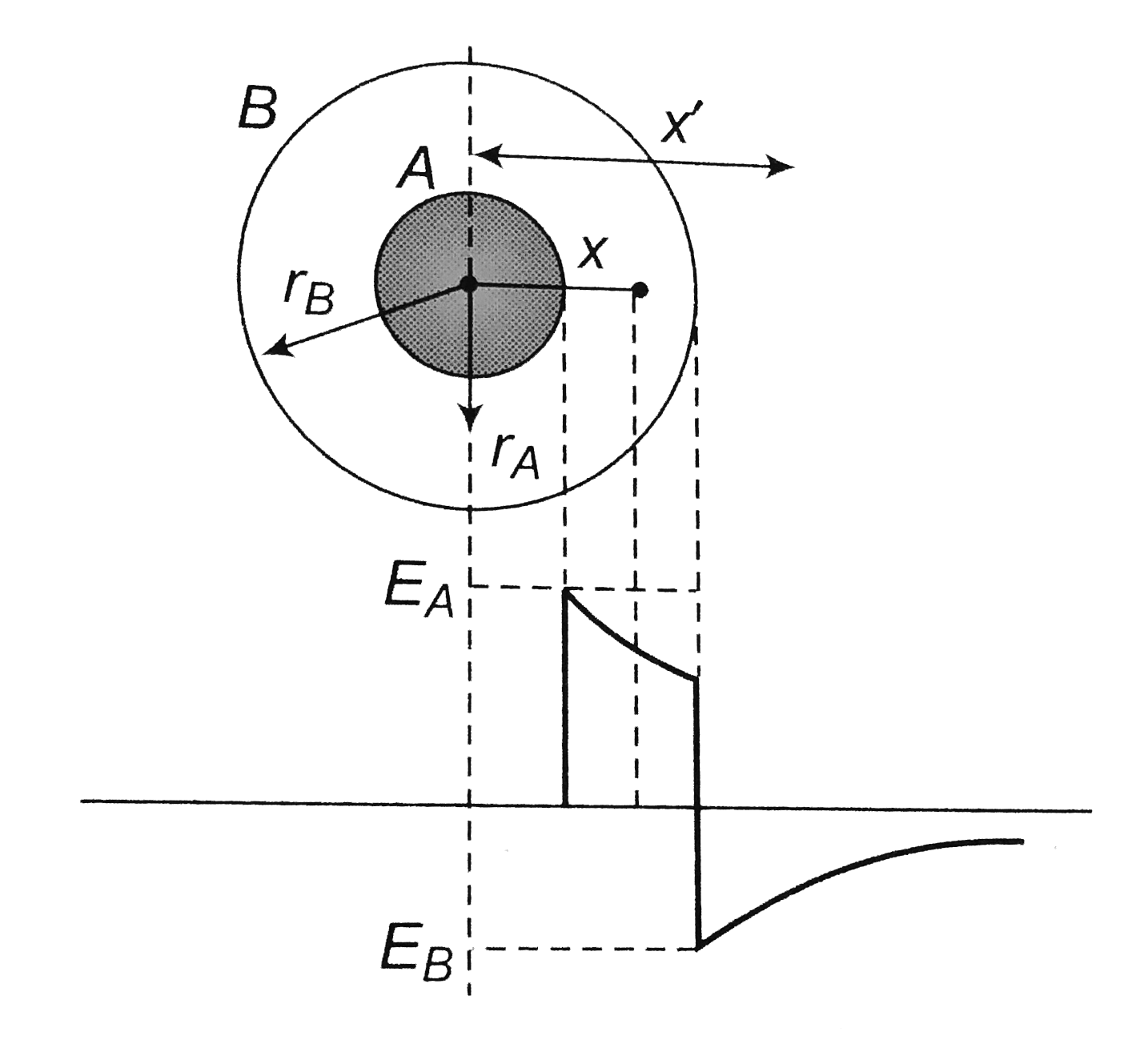
At the surface of shell A,EA=kQAr2A
Between the shell A and B, at a distance x from the common centre
E=k.QAx2 towards right hence positive
At the surface of shell B,EB=k.QAr2B towards right hence positive. Outside the both shell, at a distance x from the common centre Eout=k(QA−QB)x'2
hence negetive(as x' increases negative value of Eout decreases and it becomes zero at x=∞)
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Assertion Reason
Explore 7 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section D - Chapter End Test
Explore 29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:AIPMTNEET Questions
Explore 24 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Two concentric conducting thin spherical shells A andB having radii rA and r8(r8>rA) are charged to QA and −QB(|QB|>|QA|). The electric field strength along a line passing through the centre varies with the distance x as :
View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
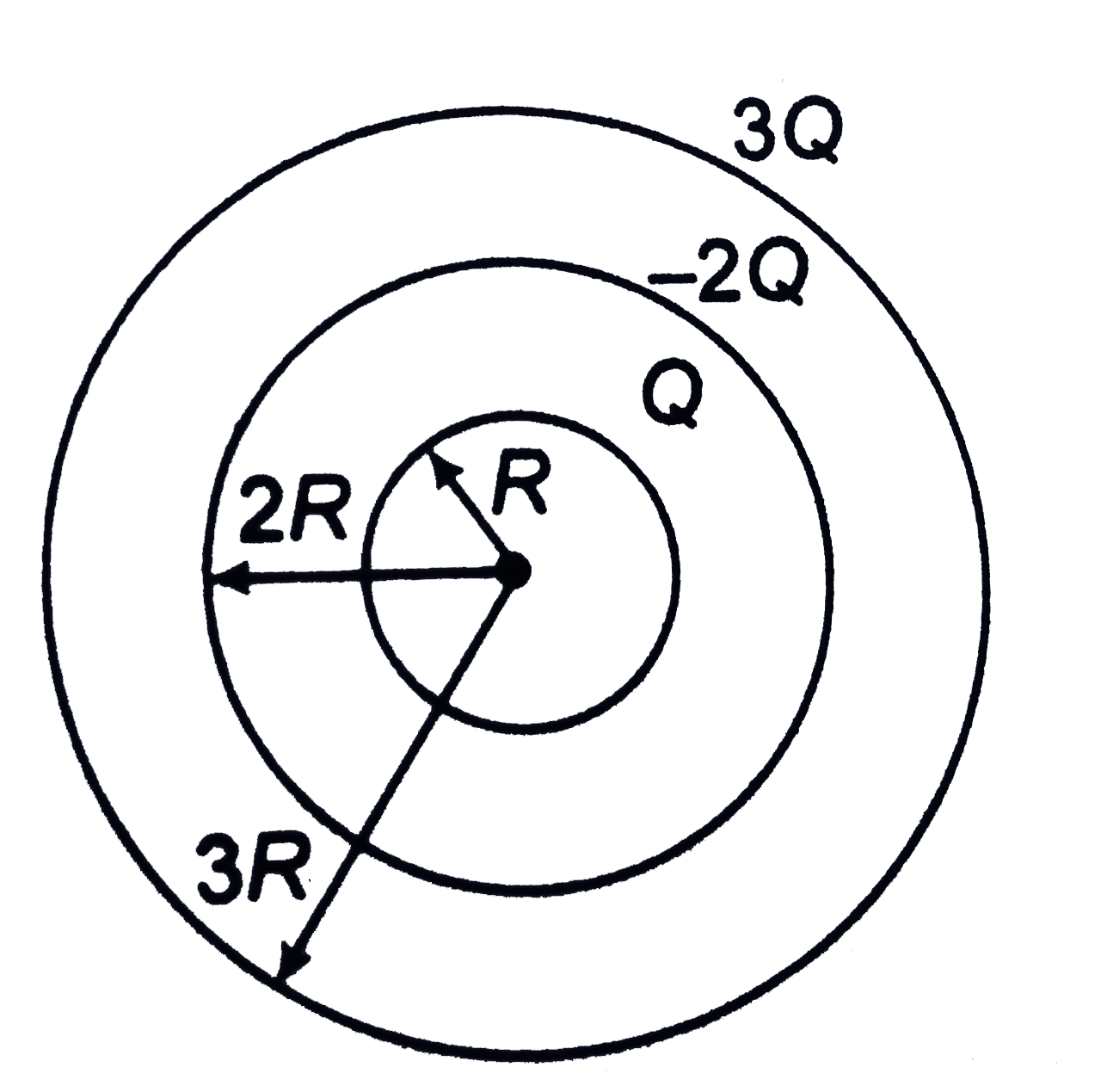
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre. ltbr> b. Compute the electric field at r=52R
c.computethe→tale≤ctrostatice≠rgys→red∈thesystem.<br>The∈≠rshellisnowco∩ected→theexternalo≠byaconduct∈gwire,passingthroughaverysmallho≤∈them≤shell.<br>Computethechar≥sonthespheresofradiiRand3R.<br>e.Computethee≤ctricfieldatr=5/2R.
View Solution
Knowledge Check
Two concentric conducting thin spherical shells A andB having radii rA and r8(r8>rA) are charged to QA and −QB(|QB|>|QA|). The electric field strength along a line passing through the centre varies with the distance x as :
A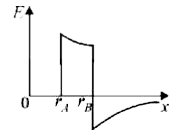 B
B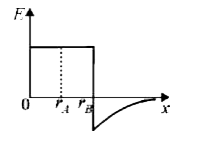 C
C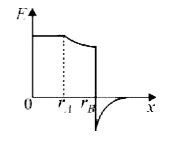 D
D
two concentric conducting thin spherical shells A and B having radii rAandrB(rB>rA are charged to QA and QA and (−QB/QBl>/QA/) . The electrical field along a line (passing through the centre) is
 A
A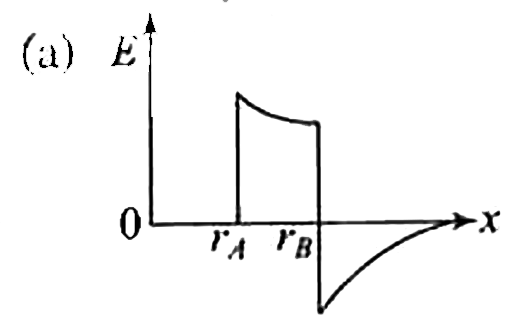 B
B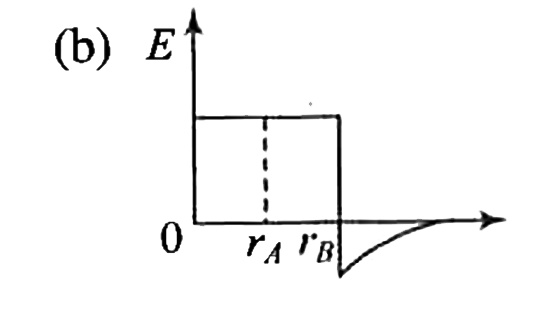 C
C D
D
Two concentric thin conducting sphereical shells having radii R and 2R are as shown in the figure .A charge +Q is given to the shell A and −4Q is given to the shell B .If A and B are connected by a thin conducting wire then the amount of heat produced after the connection is
 A3Q24πε0RBQ216πε0RC5q28πε0RDQ28πε0R
A3Q24πε0RBQ216πε0RC5q28πε0RDQ28πε0R
There are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View SolutionFigure shows three concentric thin conducting spherical shells A, B and C of radii R, 2R and 3R. The shell B is earthed A and C are given charges q and 2q respectively. Find the charges appearing on all the surface of A,B and C.

[inner surface (A)0,(B)−q,(C)43q
Outer surface (A)q,(B)−43q,(C)23q]
View SolutionTwo concentric conducting shells A and B are of radii R and 2R. A charge +q is placed at the centre of the shells. Shell B is earthed and a charge q is given to shell A. Find the charge on outer surface of A and B.
View SolutionTwo thin cocentric and coplanar spherical shells , of radii 'a' and 'b' (b>a), carry charges q and Q respectively. Find the magnitude of the electric at a point distant x from their common centre for
0<x<a,
(b) a≤x≤b,
(c) b≤x<∞
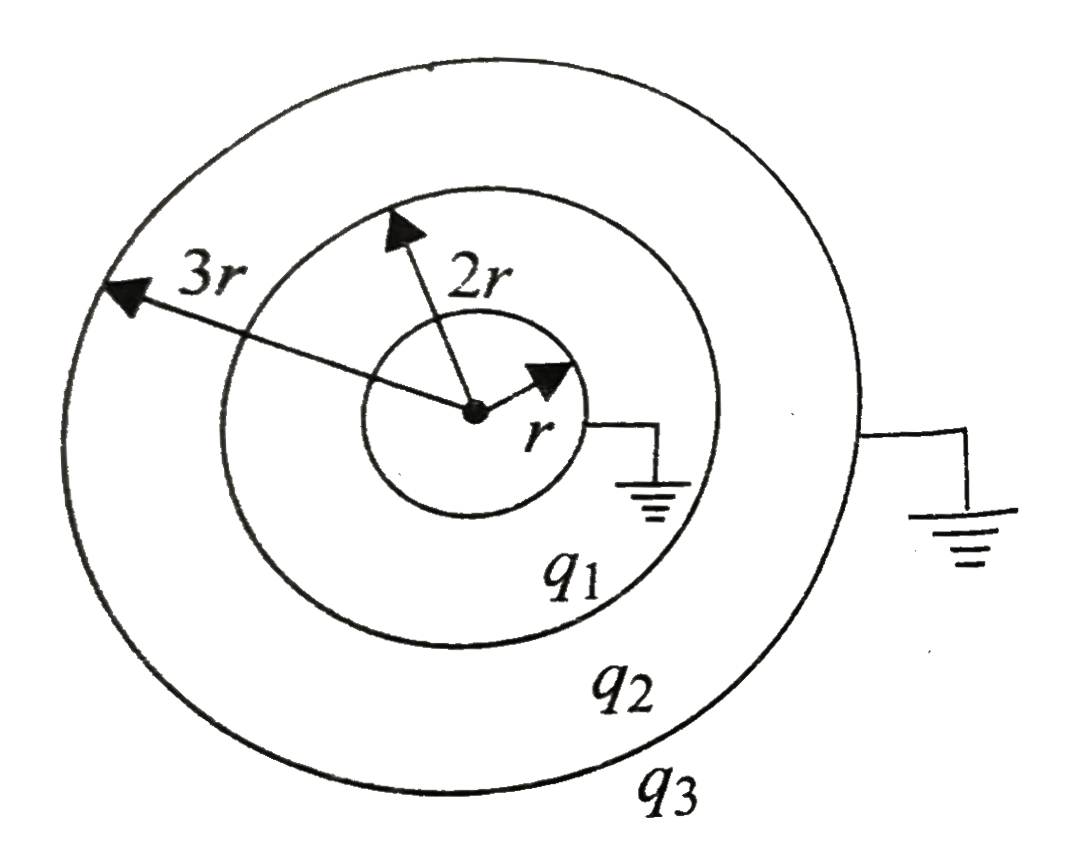
View SolutionThree concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
View Solution

