The point charges +q,−2q and +q are placed at point (x=0,y=a,z=0),(x=0,y=0,z=0) and (x=a,y=0,z=0), repectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
√2qa along +y direction
√2qa along the line joining points (x−0,y=0,z=0) and (x=a,y=a,z=0)
qa along the line joining points (x=0,y=0,z=0) and (x=a,y=a,z=0)
√2qa along +x direction
The correct Answer is:b
Electric dipole moment is a vector quantity directed from negative charge to the similar positive charge.
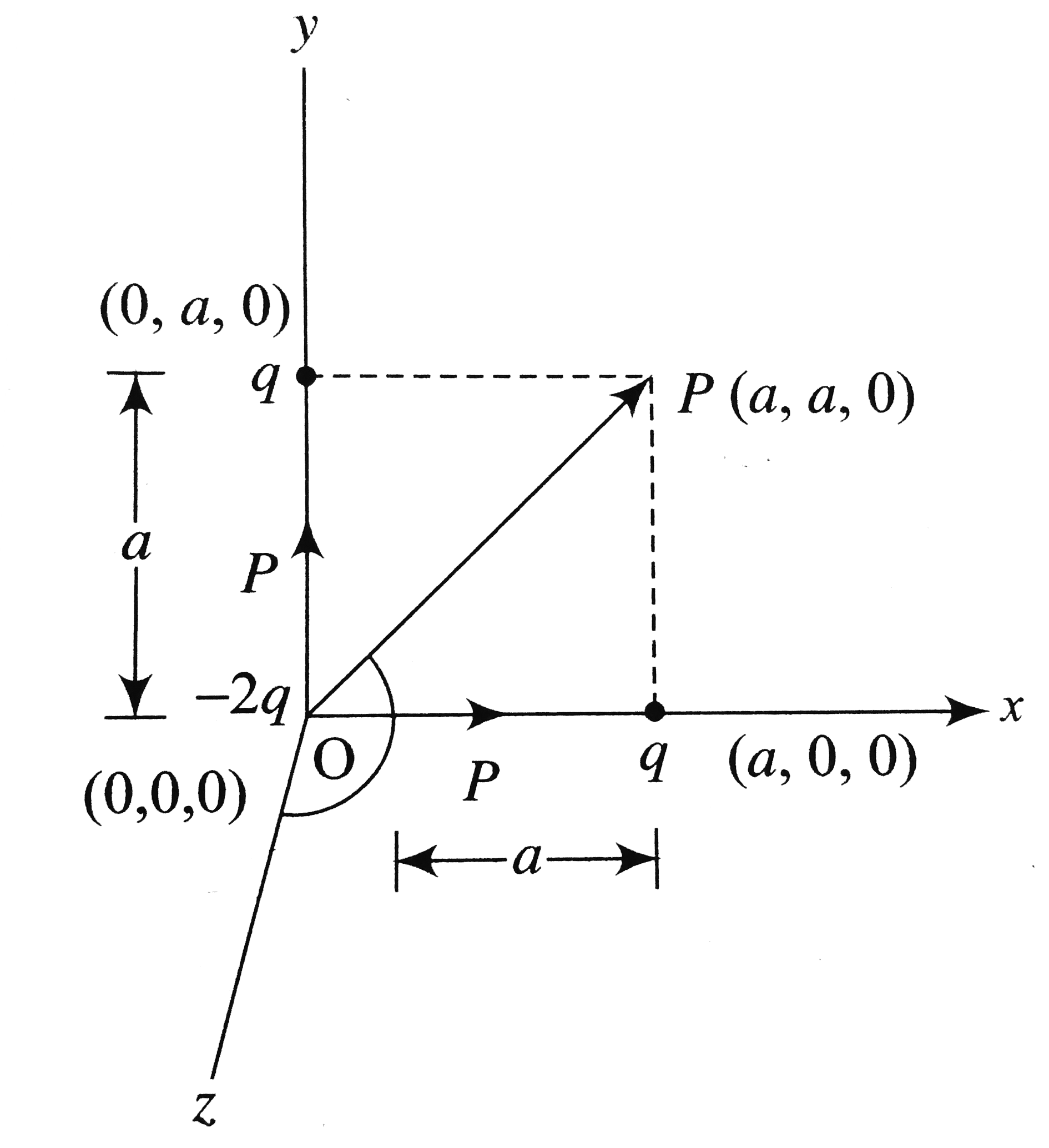
Choose the three coordinate axes as x,y and z and plot the charges with the given coordinates as shown.
O is the origin at which −2q charge is placed. The system is equivalent to two dipole along x and y-direction respectively. The dipole moments of two dipoles are shown in the figure.
The resultant dipole moment will be directed along OP where P=(a,a,0). The magnitude of resultant dipole moment is
P'=√P2+P2=√(qa)2+(qa)2=√2qa
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:AIIMS Questions
Explore 26 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Assertion Reason
Explore 7 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section B - Assertion Reasoning
Explore 25 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Two charges +q and -q are kept at (−x1,0)and(x1,0) respectively in the x-y plane. Find the magnitude and direction of the net electric field at the origin (0,0)
View SolutionTwo charges - q and +q are located at points (0, 0, - a) and (0,0, a), respectively.
What is the electrostatic potential at the points (0, 0, z) and (x, y,0) ?
View Solution
Knowledge Check
Three point charges +q, -2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0, y = 0, z = 0) and (x = a, y = 0, z = 0), respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
A√2qa along +y directionB√2qa along the line joining points
(x = 0, y = 0, z = 0)
and (x = a, y = a, z = 0)Cqa along the line joining points
(x = 0, y = 0, z = 0)
and (x = a, y = a, z = 0)D√2qa along +x directionThree point charges +q, -2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0, y = 0, z = 0) and (x = a, y = 0, z = 0), respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
A√2qa along +y directionB√2qa along the line joining points
(x = 0, y = 0, z = 0)
and (x = a, y = a, z = 0)Cqa along the line joining points
(x = 0, y = 0, z = 0)
and (x = a, y = a, z = 0)D√2qa along +x directionThree point charges +q, –2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0,y = 0, z = 0) and (x = a, y = 0, z = 0) respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are:-
A√2 qa along + x directionB√2 qa along + y directionC√2 qa along the line joining points (x=0,y=0,z=0) and (x=a,y=a,z=0)Dqa along the line joining points (x=0,y=0,z=0) and (z=a , y=a ,z=0)
for every point (x,y,z) on the y-axis: (A) x=0,y=0 (B) x=0,z=0 (C) y=0,z=0 (D) y≠0,x=0,z=0
View SolutionThree charges -1, +q and +q are situated in x-y plane at points (0, -a)(0,0) and (0, a) respectively. The potential at a point distant r(r>a) in a direction making an angle θ from y - axis will be
View SolutionThree charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
View SolutionAsserions: Two points charges +Q and −Q are fixed at point A(+a,0,0)and point B(−a,0,0) respectively.Then the magnitude of electric flux due to electric field of either point charge through infinite y-zplane (that is x=0 plane) is less than magnitude of net electric flux due to electric field of both charges through that plane (x=0 plane)
Reason :the magnitude of the net electric flux through a surface due to a system of point charges is equal to sum of magnitude of electric flux through that surface due to each of the point charge of the system.
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) resepctively.The electric potential at point (0,0,z)is (Z>a)
View Solution

