The number of electrons to be put on a spherical conductor of radius 0.1m to produce an electric field of 0.036N/C just above its surface is
2.7×105
2.6×105
2.5×105
2.4×105
The correct Answer is:C
To find the number of electrons that need to be put on a spherical conductor of radius 0.1m to produce an electric field of 0.036N/C just above its surface, we can follow these steps:
Step 1: Understand the relationship between electric field and charge
The electric field E just outside the surface of a charged spherical conductor is given by the formula:
E=k⋅Qr2
where:
- E is the electric field,
- k is Coulomb's constant (9×109N m2/C2),
- Q is the total charge on the conductor,
- r is the radius of the conductor.
Step 2: Rearranging the formula to find Q
We can rearrange the formula to solve for Q:
Q=E⋅r2k
Step 3: Substitute the known values
Given:
- E=0.036N/C
- r=0.1m
Substituting these values into the equation:
Q=0.036⋅(0.1)29×109
Step 4: Calculate Q
Calculating Q:
Q=0.036⋅0.019×109=0.000369×109=4×10−11C
Step 5: Calculate the number of electrons
The charge of a single electron is approximately 1.6×10−19C. To find the number of electrons n, we use the formula:
n=Qe
where e is the charge of one electron.
Substituting the values:
n=4×10−111.6×10−19≈2.5×108
Final Answer
The number of electrons to be put on the spherical conductor is approximately 2.5×108.
---
The electric field E just outside the surface of a charged spherical conductor is given by the formula:
E=k⋅Qr2
where:
- E is the electric field,
- k is Coulomb's constant (9×109N m2/C2),
- Q is the total charge on the conductor,
- r is the radius of the conductor.
We can rearrange the formula to solve for Q:
Q=E⋅r2k
Given:
- E=0.036N/C
- r=0.1m
Q=0.036⋅(0.1)29×109
Calculating Q:
Q=0.036⋅0.019×109=0.000369×109=4×10−11C
The charge of a single electron is approximately 1.6×10−19C. To find the number of electrons n, we use the formula:
n=Qe
where e is the charge of one electron.
n=4×10−111.6×10−19≈2.5×108
The number of electrons to be put on the spherical conductor is approximately 2.5×108.
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Electric Field And Motion
Explore 37 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Electric Field And Gauss'S Law
Explore 25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section D - Chapter End Test
Explore 29 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
A particle having the same charge as of electron moves in a circular path of radius 0.5 cm under the influence of a magnetic field of 0.5 T. If an electric field of 100V/m makes it to move in a straight path, then the mass of the particle is ( Given charge of electron =1.6×10−19C)
View SolutionA current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n
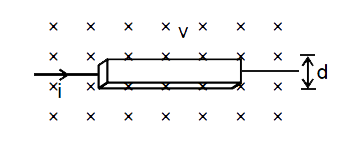
Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons.
View Solution
Knowledge Check
The electric field at the surface of a charged spherical conductor is 10 KV//m. The electric field at a distance equal to the diameter from its centre will be -
A2.5 V/mB2.5 KV/mC5.0 KV/mD5.0 V/mThe electric field at the surface of a charged spherical conductor is 10 kV/m. The electric field at an outward radial distance equal to the radius from its surface will be
A1.5 kWB2.5 kV/mC4kV/mD5kV/mA spherical conducting shell of radius r0 carry a charge q0. Then value of electric field inside it is :-
Akq0/r2Bkq0/r3CzeroDuniform but non zero
The surface charege density for a spherical conductor is 2μC/m2. Calculate electric potential of the conductor, assuming its radius to be 0.2 m.
View SolutionCalculate the earth's potential. Assume earth has a surface charge density of 1ectron/metre2.(Given,the electronic charge = −1.6×10−19C, earth's radius =6.4×106m,e0=8.9×10−12c2/Nm2)
View SolutionNet electric flux through a sphere of radius 1 m placed in a uniform electric field as shown in the figure is → E = 103 N/C
View SolutionSTATEMENT-1 : In any condition the electric field inside a conductor is always zero.
STATEMENT-2 : Under electrostatic condition, conductor is a equipotential volume.
STATEMENT-3 : Electric field just outside a conducting surface is σ2∈0
View SolutionThe electric intensity on the surface of a charged conductor of area 0.5 m2 is 200 V/m. if the electric flux is 86.6 Nm2/C, then the angle between the normal drawn to the surface and the electric intensity is
View Solution