Two charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
4.5×106N/C directed towards +5μC
4.5×106N/C directed towards +10μC
13.5×106N/C directed towards +5μC
13.5×106N/C directed towards +10μC
The correct Answer is:A
To find the net electric field at the midpoint between two charges +5μC and +10μC that are placed 20cm apart, we can follow these steps:
Step 1: Understand the Setup
- We have two charges:
- Charge q1=+5μC=5×10−6C
- Charge q2=+10μC=10×10−6C
- The distance between the charges is 20cm=0.2m.
- The midpoint between the two charges is 10cm=0.1m from each charge.
Step 2: Calculate the Electric Field Due to Each Charge at the Midpoint
The electric field E due to a point charge is given by the formula:
E=k⋅|q|r2
where k=9×109N⋅m2/C2 (Coulomb's constant), q is the charge, and r is the distance from the charge to the point where the electric field is being calculated.
Electric Field Due to q1 (5 μC):
- Distance r=0.1m
E1=9×109⋅5×10−6(0.1)2
E1=9×109⋅5×10−60.01
E1=9×5×103=45×103N/C=4.5×106N/C
Electric Field Due to q2 (10 μC):
- Distance r=0.1m
E2=9×109⋅10×10−6(0.1)2
E2=9×109⋅10×10−60.01
E2=9×10×103=90×103N/C=9×106N/C
Step 3: Determine the Direction of the Electric Fields
- The electric field due to both charges will point away from the charges since they are both positive.
- Therefore, at the midpoint:
- The electric field E1 due to +5μC will point to the right.
- The electric field E2 due to +10μC will point to the left.
Step 4: Calculate the Net Electric Field
Since E2 is greater than E1, the net electric field Enet will be:
Enet=E2−E1
Enet=9×106−4.5×106=4.5×106N/C
Final Answer
The net electric field at the midpoint between the two charges is:
Enet=4.5×106N/C
---
- We have two charges:
- Charge q1=+5μC=5×10−6C
- Charge q2=+10μC=10×10−6C
- The distance between the charges is 20cm=0.2m.
- The midpoint between the two charges is 10cm=0.1m from each charge.
The electric field E due to a point charge is given by the formula:
E=k⋅|q|r2
where k=9×109N⋅m2/C2 (Coulomb's constant), q is the charge, and r is the distance from the charge to the point where the electric field is being calculated.
- Distance r=0.1m
E1=9×109⋅5×10−6(0.1)2
E1=9×109⋅5×10−60.01
E1=9×5×103=45×103N/C=4.5×106N/C
- Distance r=0.1m
E2=9×109⋅10×10−6(0.1)2
E2=9×109⋅10×10−60.01
E2=9×10×103=90×103N/C=9×106N/C
- The electric field due to both charges will point away from the charges since they are both positive.
- Therefore, at the midpoint:
- The electric field E1 due to +5μC will point to the right.
- The electric field E2 due to +10μC will point to the left.
Since E2 is greater than E1, the net electric field Enet will be:
Enet=E2−E1
Enet=9×106−4.5×106=4.5×106N/C
The net electric field at the midpoint between the two charges is:
Enet=4.5×106N/C
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Motion
37 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Gauss'S Law
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Two charges ±10μC are placed 5⋅0mm apart. Determine the electric field at (a) point P on the axis of dipole 15cm away from its center on the side of the positive charge. As shown in Figure and at (b) a point Q. 15cm away form O on a line passing through O and a line passing through O and normal to the axis of the dipole as shown in Fig.
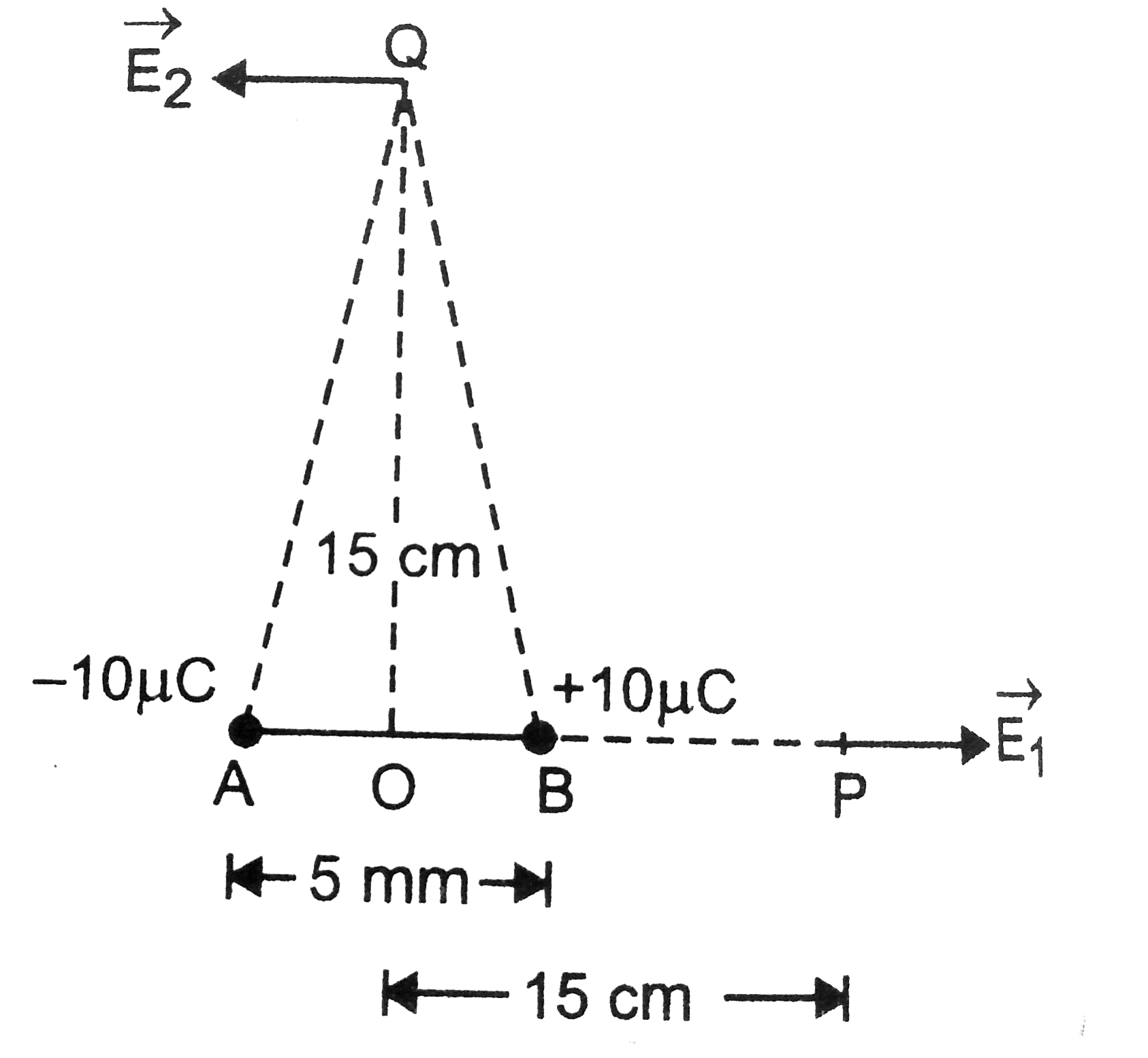
View SolutionA and B are two points separated by a distance 5cm.Two charges 10μC and 20μC are placed at A and B.The resultant electric intensity at a point P outside the charges at a distance "5cm from 10μC is
View Solution
Knowledge Check
Two tiny spheres carrying charges 1.8μCand2.8μC are located at 40 cm apart. The potential at the mid-point of the line joining the two charges is
A3.8×104VB2.1×105VC4.3×104VD6.3×105VTwo tiny spheres carrying charges 1.8μCand2.8μC are located at 40 cm apart. The potential at the mid-point of the line joining the two charges is
In the above question, the potential at a point20cm from the mid-point of the line joining the two charges in a place normal to the line and passing through the mid-point isA1.4×105VB4.2×103VC2.9×104VD3.7×105VTwo point charges q1=4μC and q2=9μC are placed 20cm apart. The electric field due to them will be zero on the line joining them at distamce of
A8cm from q1B8cm from q2C8013cm from q1D8013cm from q2
Two tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View SolutionTwo tiny spheres carrying charges 1.5μCand2.5μC are located 30 cm apart. Find the potential and electric field:
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this mid-point in a plane normal to the line and passing through the mid point.
View SolutionTwo charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
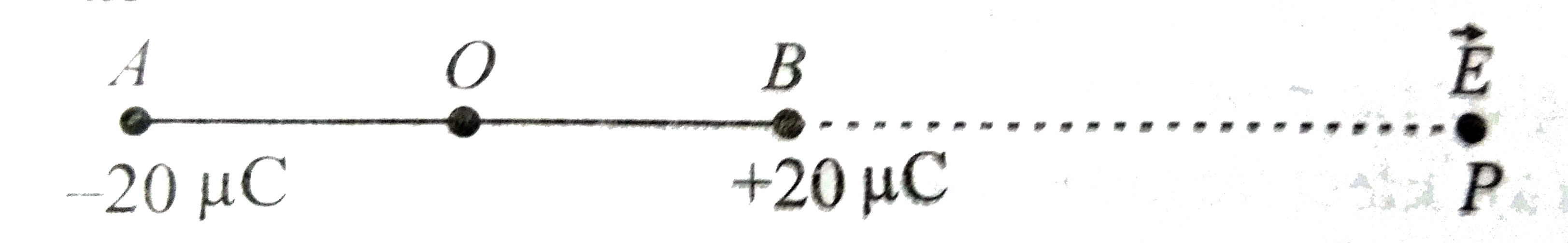
View SolutionA and "B" are two points separated by a distance "5cm" Two charges 10μC and 20μC are placed at "A" and "B" .The resultant electric intensity at a point "P" outside the charges at a distance "5cm" from "10μC" is
View SolutionTwo positive charges of 1mu Cand2 mu C are placed 1 metre apart. The value of electric field in N/C at the middle point of the line joining the charge will be :
View Solution
