In the given figure two tiny conducting balls of identical mass and identical charge hang from non-conducting threads of equal length . Assume that is so small that than , then for equilibrium is equal to
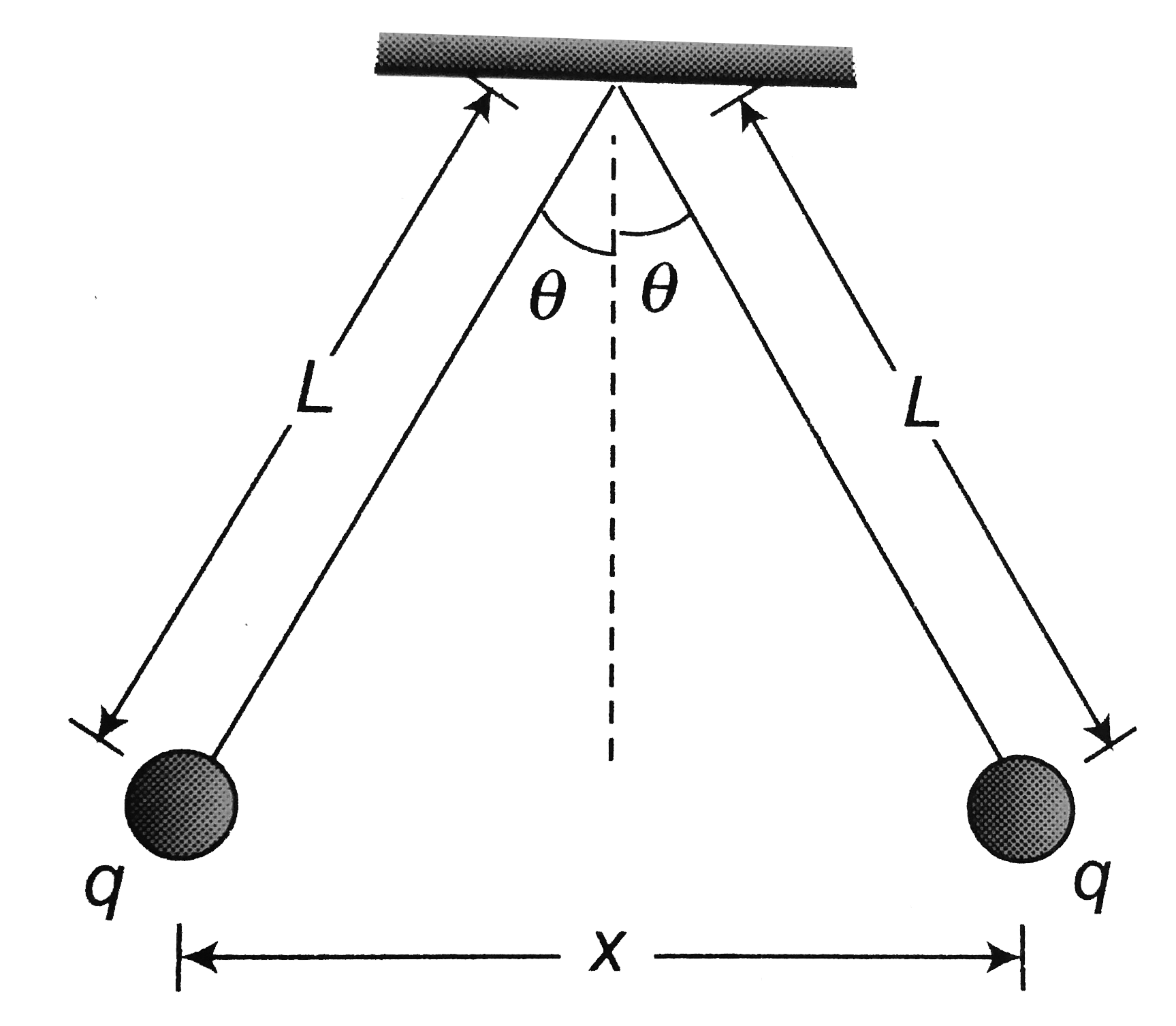
The correct Answer is:a
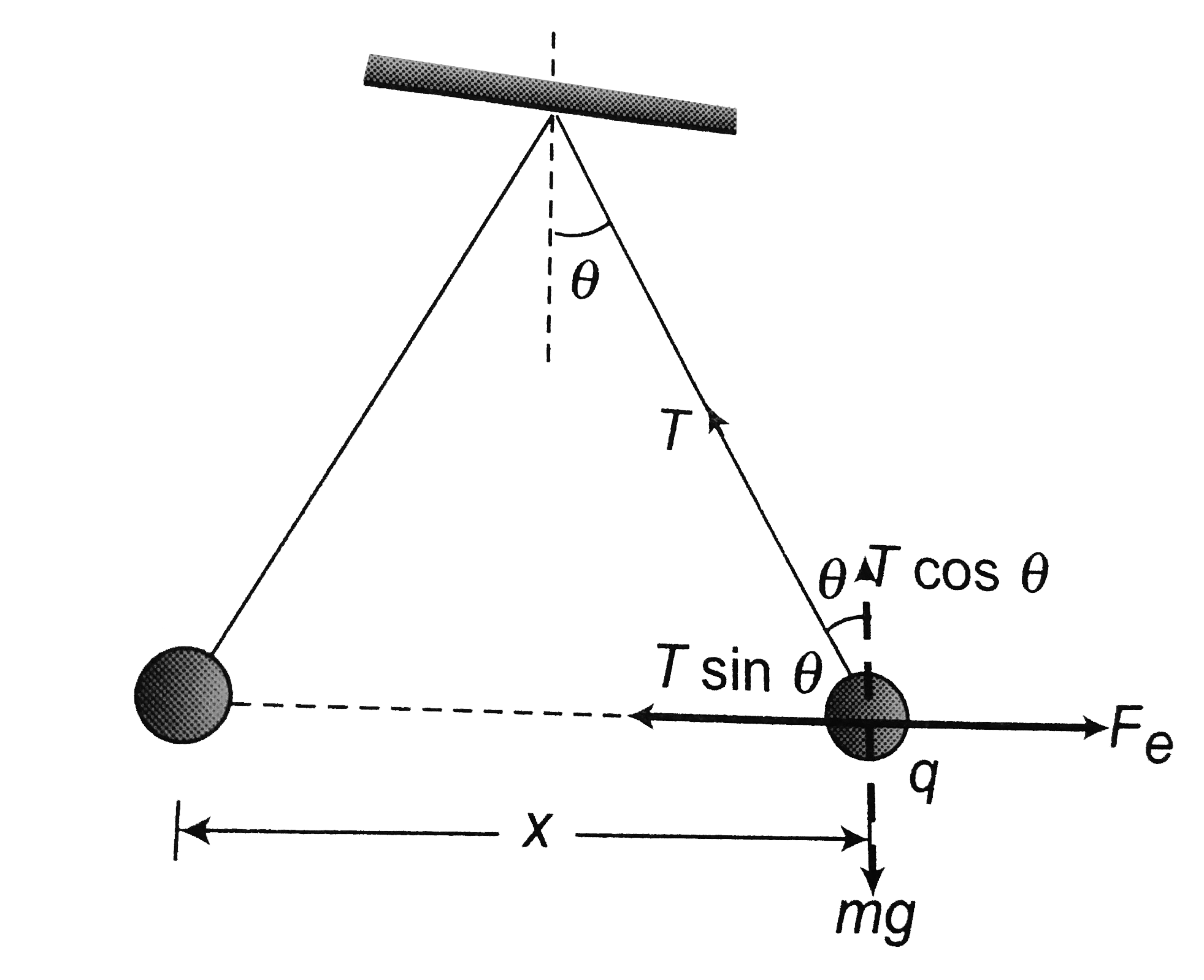
In equilibrium ….(i)
….(ii)
Hence
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field Due To Point Charge
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Motion
37 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Two identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View Solution
Knowledge Check
If a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
Aε0(mgq)tanθBε0(2mgq)tanθCε0(mgq)tanθDε0(mg3q)tanθIf a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vectical charged conductinb plate, then for equilibrium of sphere the surface charge density of the plate -
Aε0mgtanθqB(2ε0mgtanθ)/qCε0mgqtanθDε0mgtanθ3qTwo identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
Ax=(q2l2πε0mg)1/2Bx=(q2l2πε0mg)1/3Cx=(q2l22πε0m2g)1/3Dx=(q2l22πε0m2g2)1/3
Two idential pith balls , each of mass m and charge +q. are suspended from a point with threads of length l each. If in equiilbrium state θ be the angle which each thread makes with vertical in equilibrium , find value of charge on each ball.
View SolutionA small non-conducting ball of mass m=1mg and charge q=2×10−8C hangs from an insulating thread that makes an angle θ=30∘ with vertical uniformly charged non-conducting sheet.Considering the gravitational force on the ball and assuming that the sheet extends for vertically and into out of the page.Calculate surface charge density of sheet.
View SolutionTwo small balls, each having charge q, are suspended by two insulating threads of equal length L fron a hook in an elevator. The elevator is freely falling. Calculate the angle etween the two threads and tension in each thread.
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution
