एक समद्विबाहु त्रिभुज ABC इस प्रकार है की AB =AC तथा बड़ी हुई भुजा CB पर एक बिंदु E इस प्रकार है की EF⊥AC यदि AD⊥BC हो, तो सिद्ध करो की ΔABD~ΔECF
समद्विबाहु त्रिभुज ABC में दिया है की AB = AC
∴ ∠B=∠C
Δ'sABD
∴ ∠B=∠C
Δ'sABD तथा ECF में
∠ABD=∠ECF [∵∠B=∠C]
∠ADB=∠EFC=90∘ [∵AD⊥BC तथा EF⊥AC ]
अतः समरूपता की AA कसौटी से
ΔABD~ΔECF
Topper's Solved these Questions
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.1
12 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.2
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - बहु विकल्पीय प्रश्न
28 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - RD SHARMACHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - बहु विकल्पीय प्रश्न
16 Videos
Similar Questions
कोष्ठक में दिए हुए शब्दों में से ही शब्दों को चुनकर रिक्त स्थान को भारिये:
सभी वृत.......(सर्वांगसम, समरूप) होते है|
View Solutionत्रिभुज ABC की भुजाओं AB और AC बिंदु D और E इस प्रकार है की DE भुजा BC के समानांतर है| यदि|||
AD=6 सेमि , DB = 9 सेमि तथा AE =8 सेमि, हो तो AC ज्ञात करो|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View Solutionआकृति 6.40 में , AB =AC वाले , एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है यदि AD⊥BC और EF⊥AC है तो सिद्ध कीजिए की ΔABD~ΔECF है
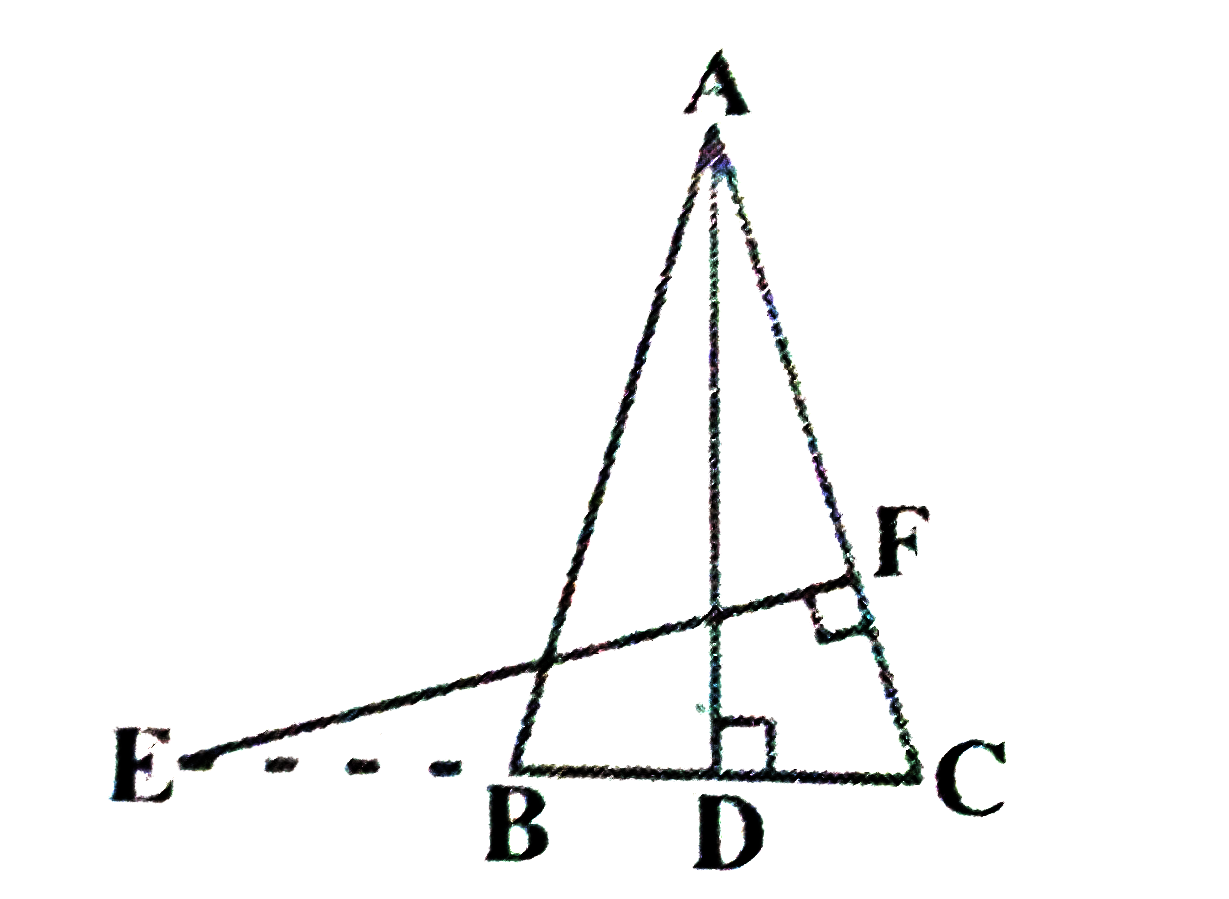
View SolutionIn the given figure, E is a point on side CB produced of an isosceles ΔABC with AB=AC.. If AD⊥BCandEF⊥AC, prove tha ΔABD~ΔECF
View SolutionIn △ABC, AB=AC and AD⊥BC,BE⊥AC and CF⊥AB. Then △ABC is symmetrical about
View SolutionIn Fig., E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that △ABD~△ ECF.
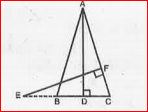 .
.
View SolutionDelta ABC And Delta ABD In AC = BD and DA bot AB, CB bot AB Which of the following statements is true? Delta ABC ~= Delta ABD
View Solutionਚਿੱਤਰ 6.40 ਵਿਚ,AB= AC ਵਾਲੇ ਇਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਵਧਾਈ ਗਈ ਭੁਜਾ CB ਉੱਤੇ ਸਥਿਤ E ਇਕ ਬਿੰਦੂ ਹੈ। ਜੇਕਰ AD⊥BC ਅਤੇ EF⊥AC ਹੋਵੇ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ ΔABD~ΔECF ਹੈ।
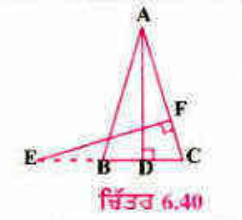
View Solutiontriangle ABC is an isosceles triangle with AB = AC=13 cm. AD is the median on BC from A such that AD= 12 cm. The length of BC is equal to: triangle ABC में, AB = AC = 13 सेमी के साथ एक सममद्विबाहु त्रिभुज है। AD, A से BC पर माध्यिका इस प्रकार है की AD = 12 सेमी। BC की लंबाई है:
View SolutionIn an isosceles triangle ABC, AB=AC and AD is perpendicular to BC at D. If AD = 8 cm and perimeter of triangle ABC is 64cm, then the area of triangle ABC एक समद्विबाहु त्रिभुज ABC में, AB= AC और AD, BC पर लंबवत है। यदि AD =8 सेमी और ABC की परिधि 64 cm है, तो ABC का क्षेत्रफल है:
View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View SolutionIn triangle ABC , AD bot BC and BE bot AC , AD and BE intersect each other at F. If BF = AC, then the measure of angle ABC is: त्रिभुज ABC में, AD bot BC है तथा BE bot AC है | AD और BD एक दूसरे को F पर काटते है | यदि BF = AC है, तो angle ABC का माप क्या होगा ?
View SolutionIn a △ABC, D and E are two points on the sides AB and BC , respectively such that AD : DB = 2: 3 and DE || AC. If the area of △ADE is equal to 18 square cm, then what is the area ( In square cm) of △ABC ?
किसी त्रिभुज ABC में, D और E क्रमश: भुजा AB और BC पर स्थित बिंदु हैं जो इस प्रकार हैं कि AD : DB = 2: 3 है तथा 9DE || AC है | यदि त्रिभुज ADE का क्षेत्रफल 18 वर्ग सेमी के बराबर है, तो त्रिभुज ABC का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें
View Solution
