चित्र में यदि AD,∠BAC का अन्तः समद्विभाजक है तथा AB = 10 सेमि, AC =14 सेमि, और BC =6 सेमि, हो तो BD और DC की लम्बाईयाँ ज्ञात करों|
माना BD =x सेमि, तो DC = 6 -x सेमि
हम जानते है की त्रिभुज के किसी कोण का अंत समद्विभाजक सम्मुख भुजा को उस कोण को बनाने वाली भुजाओं के अनुपात में अन्तः विभाजित करता है| चित्र में AD,∠A का समद्विभाजक है|
∴ ABAC=BDDC
⇒ 1014=x6−x
⇒ 57=x6−x
⇒ 5(6−x)=7x
⇒ 30−5x=7x
⇒ 12x=30
⇒ x=3012=2.5 सेमि
अतः BD=2.5 सेमि., तथा DC=(6−x) सेमि. =( 6 -2 .5 ) सेमि = 3 .5 सेमि.

Topper's Solved these Questions
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.1
12 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.2
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - बहु विकल्पीय प्रश्न
28 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - RD SHARMACHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - बहु विकल्पीय प्रश्न
16 Videos
Similar Questions
कोष्ठक में दिए हुए शब्दों में से ही शब्दों को चुनकर रिक्त स्थान को भारिये:
सभी वृत.......(सर्वांगसम, समरूप) होते है|
View Solutionत्रिभुज ABC की भुजाओं AB और AC बिंदु D और E इस प्रकार है की DE भुजा BC के समानांतर है| यदि|||
AD=6 सेमि , DB = 9 सेमि तथा AE =8 सेमि, हो तो AC ज्ञात करो|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View Solutionएक पुस्तकालय को एक शेल्फ में दो भिन्न प्रकार की पुस्तकें रखनी है| पुस्तकें क्रमशः 6 सेमि और 4 सेमि मोती है| तथा उसका भार क्रमशः 1 किग्रा और 112 किग्रा है| शेल्फ 96 सेमि लम्बी है तथा अधिकतम 21 किग्रा भार सेह सकती है|शेल्फ दो प्रकार की पुस्तकों से किस प्रकार भरा जाएँ ताकि उसमें अधिकतम पुस्तकें रखी जा सकें?
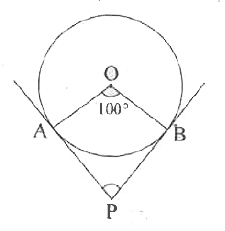
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View SolutionIn triangle ABC ,AD is the bisector of angle BAC , meeting BC at D. If AC= 21 cm, BC = 12 cm and the length BD is 2 cm less than DC, then the length of side AB is : त्रिभुज ABC में, AD, angle BAC का द्विभाजक है जो BC से D पर मिलता है| यदि AC =21 सेमी, BC =12 सेमी है और BD की लंबाईDC से 2 सेमी कम है, तो भुजा AB की लंबाई ज्ञात करें |
View SolutionIn a triangle ABC , AD is perpendicular to BC from A, if angle BAC = 90^@ , then AB^2:AC^2 is equal to : त्रिभुज ABC में, AD, A से BC पर डाला गया लम्ब है | यदि angle BAC = 90^@ है, तो AB^2:AC^2 का मान क्या होगा ?
View SolutionIn triangle ABC , angle ABC=90^@ and BD bot AC . If AD = 4 cm and CD =5 cm, then BD is equal to: त्रिभुज ABC में, angle ABC=90^@ तथा BD bot AC है | यदि AD =4 सेमी और CD = 5सेमी है, तो BD किसके बराबर है ?
View SolutionIn △ABC ,AD is the bisector of ∠A,meets BC at D. If BC = a, AC = b and AB = c, then BD - DC=
त्रिभुज ABC में, AD, जो कोण A का समद्विभाजक है ,BC से D पर मिलता है| यदि BC = a, AC = b और AB =c है, तो BD - DC = ?
View SolutionIn △ABC AB = 7 cm, BC =10cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC, where D is a point on BC, then BD is equal to:
यदि त्रिभुज ABC में, AB = 7 सेमी, BC = 10 सेमी तथा AC =8 सेमी है | यदि AD कोण BAC का समद्विभाजक है, जहाँ D, BC पर स्थित एक बिंदु है, तो BD का मान किसके बराबर है ?
View SolutionIn ∠ABC, AB=AC and D is a point on BC. If BD = 5cm, AB =12 cm and AD = 8 cm, then the length of CD is:
त्रिभुज ABC में, AB=AC है और D, BC पर स्थित एक बिंदु है | यदि BD =5 सेमी, AB = 12 सेमी और AD = 8 सेमी है, तो CD की लंबाई ज्ञात करें |
View SolutionThe bisector of ∠B in △ABC meets AC at D. If AB = 10 cm, BC= 11 cm and AC = 14 cm, then the length of AD is:
△ABC में ∠B का समद्विभाजक AC से D पर मिलता है | यदि AB =10 सेमी, BC = 11 सेमी और AC =14 सेमी है, तो AD की लंबाई क्या होगी ?
View SolutionIn △ABD, C is the midpoint of BD. If AB = 10 cm, AD = 12 cm and AC = 9 cm, then BD =?
त्रिभुज ABD में, C, BD का मध्य बिंदु है | यदि AB = 10 सेमी, AD = 12 सेमी और AC = 9 सेमी है, तो BD = ?
View Solution
