एक वृत्त C(O, r) की दो समान लम्बाई की जीवाओ AB तथा CD को यदि आगे बढ़ाया जाये तो ये बिन्दु E पर मिलती हैं जैसा की चित्र में दर्शाया गया है । सिध्द करो कि BE=DE तथा AE=CE होगा।

दिया है : वृत्त C(O, r) की दो जिवाएँ AB तथा AC इस प्रकार हैं कि AB = CD तथा ये जिवाएँ आगे बढ़ाने पर एक दूसरे को बिन्दु E पर काटती है ।
सिध्द करना है : BE = DE तथा AE = CE
रचना : OE को मिलाया तथा O से OL⊥AB व OM⊥CD खींचा ।
उपपति : हमे दिया गया है कि :
AB = CD
⇒ OL=OM ...(i) [समान जिवाएँ केन्द्र से समान दूरी पर होती हैं ।]
∵ OL⊥AB⇒AL=LB=12AB ...(ii)
तथा OM⊥CD⇒CM=DM=12CD ...(iii)
अब ΔOLE तथा ΔOME में हम देखते हैं कि
OL = OM [समीकरण (i) से]
∠OLE=∠OME=90∘
तथा OE = OE [उभयनिष्ठ भुजा]
अत:, RHS सर्वांगसमता कसौटी से
ΔOLE≅ΔOME
⇒ LE=ME ...(iv)
[∵ सर्वांगसम त्रिभुजों के संगत भाग समान होते हैं]
⇒ LB+BE=MD+DE
⇒ 12AB+BE=12CD+DE [(ii) व (iii) से]
⇒ BE=DE [∵AB=CD∵12AD=12CD]
⇒ AB+BE=AB+DE [दोनों तरफ AB जोड़ने पर]
⇒ AB+BE=CD+DE [∵AB=CD]
⇒ AE=CE
Topper's Solved these Questions
- वृत्तBOOK - RD SHARMACHAPTER - वृत्तEXERCISE - प्रश्नावली 16.1
16 Videos
- वृत्तBOOK - RD SHARMACHAPTER - वृत्तEXERCISE - प्रश्नावली 16.2
15 Videos
- वास्तविक संख्याओं के घातांकBOOK - RD SHARMACHAPTER - वास्तविक संख्याओं के घातांकEXERCISE - बहु विकल्पीय प्रश्न
40 Videos
- संख्या पद्धति BOOK - RD SHARMACHAPTER - संख्या पद्धति EXERCISE - बहु विकल्पीय प्रश्न
21 Videos
Similar Questions
वे सभी बिन्दु जो एक वृत्त के अंदर/बाहर स्थित होते हैं, उन्हें …….. बिन्दु कहते हैं ।
View Solutionएक वृत्त की त्रिज्या 8 सेमी. है । यदि इसकी एक जीवा की लम्बाई 12 सेमी. हो, तो इस जीवा की वृत्त के केंद्र से दूरी ज्ञात करो ।
View Solution{2−3(2−3)3}3 का मान होगा:
View Solutionनिम्न में से कौन सा कथन सत्य है?
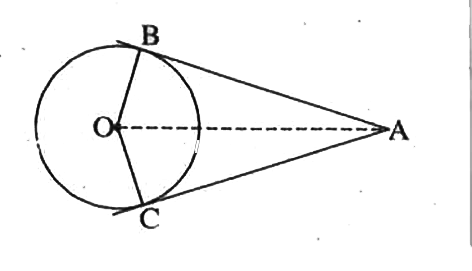
View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
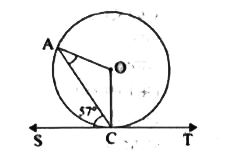
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionपाँच पासो को एक साथ फेंका गया है। यदि एक पासे पर सम अंक आने को सफलता माना जाये तो अधिकतम 3 सफलताओ कि प्रायिकता ज्ञात करो ।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि एक दीर्घवृत्त की दीर्घ अक्ष की लम्बाई, उसके लघु अक्ष की लम्बाई की तिगुनी है, तो उसकी उत्केन्द्रता होगी
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि 5m तार को 8 भागों में विभाजित करते है तो हर एक भाग की लम्बाई ज्ञात करो।
View Solution
