एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाएँ क्रमशः 9 मी, 40 मी., 28 मी तथा 15 मी लम्बाई की है और पहली दो भुजाओं के बीच का कोण समकोण है।
300 मी 2
316 मी 2
361 मी 2
306 मी 2
The correct Answer is:D
मान लीजिये ABCD दिया गया चतुर्भुज इस प्रकार है
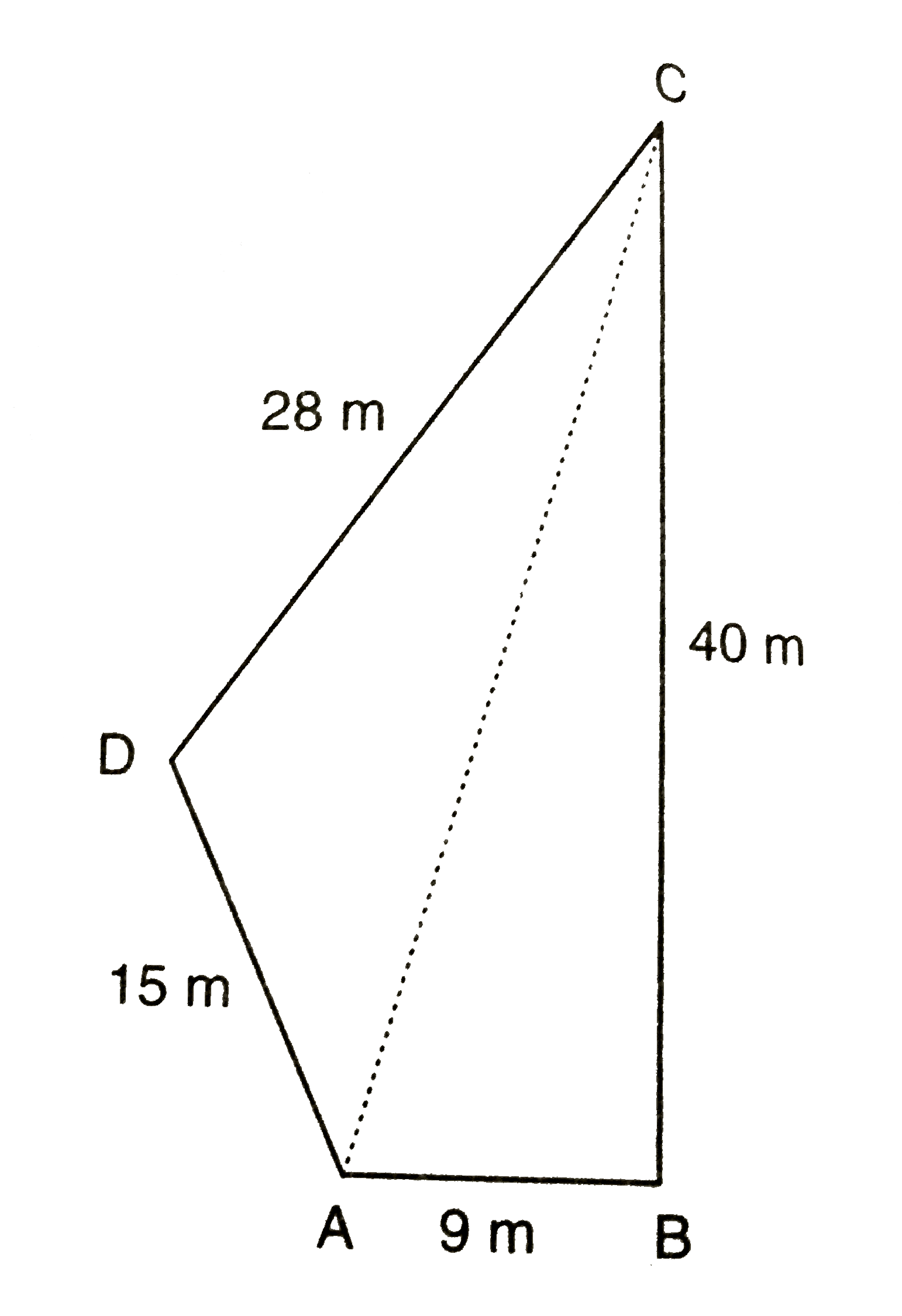
दिया हैं,
पहली दो भुजाओं के बीच का कोण समकोण है|
अतः ∠ABC=90∘
तथा AB=9मी, BC=40मी, CD=28मी, AD=15मी
चतुर्भुज ABCD का क्षेत्रफल =?
चूंकि आकृति को 2 त्रिभुजों ADC और ABC में विभाजित किया जा सकता है
अतः चतुर्भुज ABCD का क्षेत्रफल =(ΔABC का क्षेत्रफल ) + (ΔACD का क्षेत्रफल )
ΔABC से, हम AC ज्ञात कर सकते हैं|
त्रिभुज ABC में,
AC2=AB2+BC2 [पाइथागोरस प्रमेय द्वारा ]
⇒AC2=92+402=1681
⇒AC=41 मी
∴ΔABC का क्षेत्रफल = 12 (आधार × ऊँचाई )
⇒ΔABC का क्षेत्रफल = 12(AB×BC)
⇒ΔABC का क्षेत्रफल = 12(9×40) मी 2 = 180 मी 2
अब ΔACD में,
AC=41 मी, CD=28 मी. तथा DA=15 मी
माना की a=AC=41 मी, b=CD=28 मी तथा c=DA=15 मी
चूंकि अर्धपरिमाप s=a+b+c2=41+28+152=842=42
∴ΔACD का क्षेत्रफल =√s(s−a)(s−b)(s−c)
⇒ΔACD का क्षेत्रफल =√42(42−41)(42−28)(42−15)
⇒ΔACD का क्षेत्रफल = √42×1×14×27=√14×3×14×27
⇒ΔACD का क्षेत्रफल = 14×9=126 मीटर 2
अतः चतुर्भुज ABCD का क्षेत्रफल =(ΔABC का क्षेत्रफल ) + (ΔACD का क्षेत्रफल )
=(180+126) मी 2
= 306 मी 2
अतः चतुर्भुज ABCD का क्षेत्रफल 306 मी 2 हैं|
Topper's Solved these Questions
Similar Questions
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसकी भुजाएँ 150 सेमी., 120 सेमी. तथा 200 सेमी. है।
View Solutionचतुर्भुज ABCD का क्षेत्रफल ज्ञात किजीये जिसमे AB =3 सेमी. BC = 4 सेमी. CD = 4 सेमी. DA = 5 सेमी.तथा AC = 5 सेमी. |
View Solutionचित्र में, त्रिभुज ABC में ∠A समकोण है तथा AL भुजा BC पर लम्ब है । सिद्ध कीजिए कि ∠BAL=∠ACB है ।
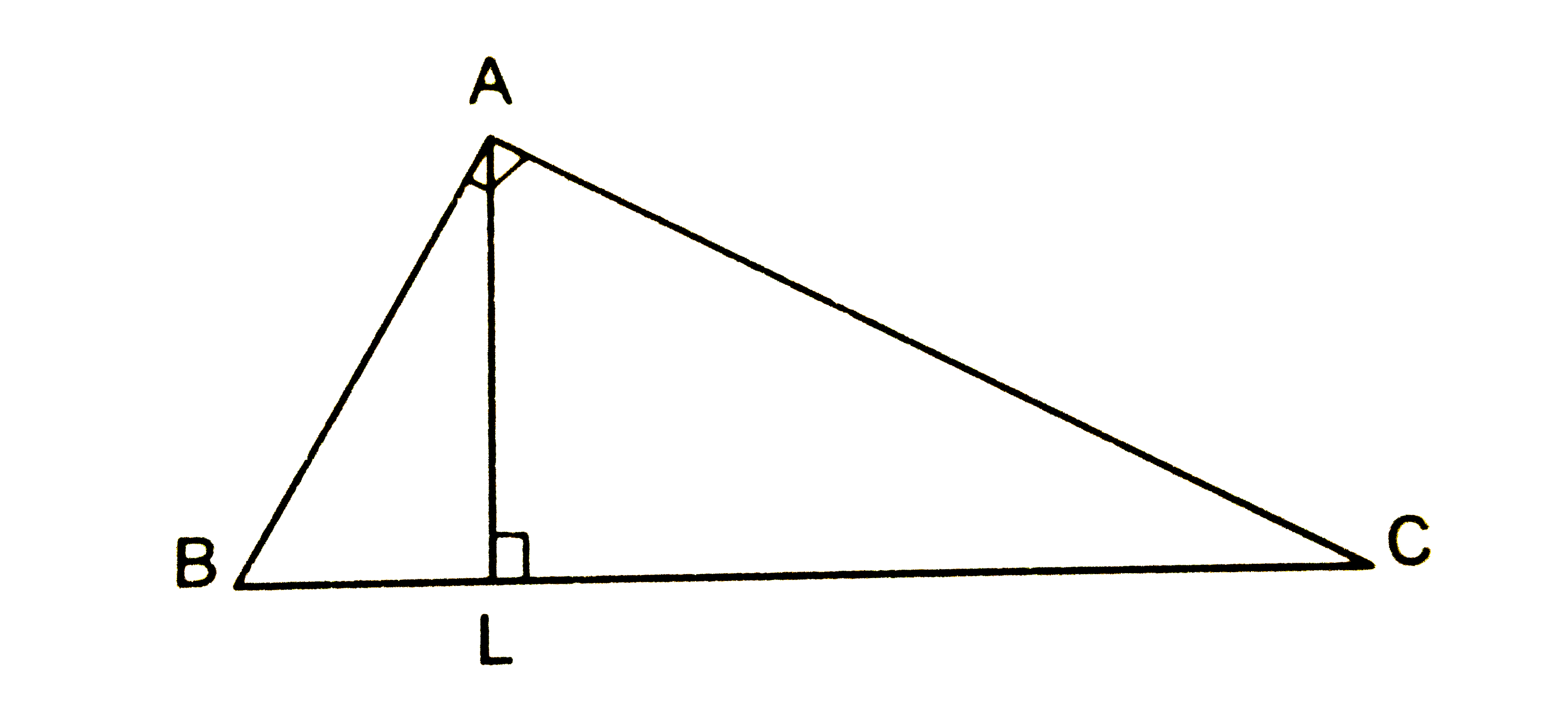
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओ के समीकरणy=ax,y=bx तथा ax+by+c=0 है
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionकिसी बेलन का अर्धव्यास 2 मी/से की दर से बढ़ता है और ऊँचाई 3 मी/से की दर से घटती है। जब उसकी ऊँचाई 5 मी और अर्धव्यास 3 मी हो, तो बेलन के आयतन के परिवर्तन की दर होगी
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
View Solution500 फेरे "सेमी"^(-1 )तथा0.5 मी व्यास वाली परिनालिका की लम्बाई 1 मी है। जब उसमे 2 एम्पियर की धारा प्रवाहित की जाती है ,तो चुम्बकीय फ्लक्स का मान कितना होगा ?
View SolutionA cube is placed inside a cone of radius 20cm and height 10cm, one of its face being on the base of the cone and vertices of opposite face touching the cone. What is the length (in cm) of side of the cube? एक घन को एक शंकु जिसकी त्रिज्या 20 से. मी. तथा ऊँचाई 10 से.मी. है, के अंदर रखा जाता है, उसको एक सतह शंकु के आधार कौर ओर है तथा विपरीत सतह के शीर्ष शंकु का स्पर्श कर रहे है। घन की भुजा लम्बाई (से. मी. में) क्या है ?
View SolutionThe height of right pyramid whose area of the base is 30m^2 and volume is 500m^3 , is ऐसे लंब पिरामिड की ऊँचाई ज्ञात कीजिए जिसके तल का क्षेत्रफल 30 मी^2 और आयतन 500 मी^3 है ।
View SolutionTwo sides of a plots measuring 32 m and 24 m and the angle between them is a perfect right angle. The other two sides measure 25 m each. and the other three angles are not right angles. The area of the plot in m^2 is - एक भूखण्ड की दो भुजाएँ 32 मी. और 24 मी. की हैं और उनके बीच का कोण पूर्ण समकोण है । अन्य दो भुजाएँ प्रति 25 मी. की हैं और अन्य तीन कोण समकोण नहीं हैं । भूखण्ड का क्षेत्रफल ( मी^2 ) में कितना होगा ?
View SolutionIf a distance of 50m is covered in 1 min, 90m in 2 min and 130 m in 3 min, find the distance covered in 15 min. यदि 50 मी. की दूरी 1 मिनट में तय की जाती है, 90 मी, की दूरी 2 मिनट में और 130 मी. की दूरी 3 मिनट में तय की जाती है, तो 15 मिनेट,में तय की जाने वाली दूरी ज्ञात कीजिए।
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solution