यदि PQ=PT तथा ∠TPS=∠QPR हो, तो सिध्द करो कि ΔPRSएक समद्विबाहु त्रिभुज है |
ΔPQTमें यह दिया है कि
PQ=PT
⇒ ∠PTQ=∠PQT....(i) [∵ समान भुजाओं के सम्मुख कोण समान होते हैं]
अतः ΔPQRतथा ΔPTSमें
PQ=PT [दिया]
∠QPR=∠TPS [दिया है]
तथा, ∠PQR=∠PTS [(i)से]
अतः कोण-भुजा-कोण सर्वागसमता कसौटी से
ΔPQR≅ΔPTS
⇒ PR=PS [∵ सर्वांगसम त्रिभुजों के संगत भाग समान होते है]
अतः ΔPRSएक समद्विबाहु त्रिभुज है |
Topper's Solved these Questions
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:प्रश्नावली 10.1
Explore 13 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:प्रश्नावली 10.2
Explore 3 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:बहु विकल्पीय प्रश्न
Explore 20 Videos
- सांखि्यिकीय आँकड़ों का सारणीयनBook:RD SHARMAChapter:सांखि्यिकीय आँकड़ों का सारणीयनExercise:बहु विकल्पीय प्रश्न
Explore 10 Videos
Similar Questions
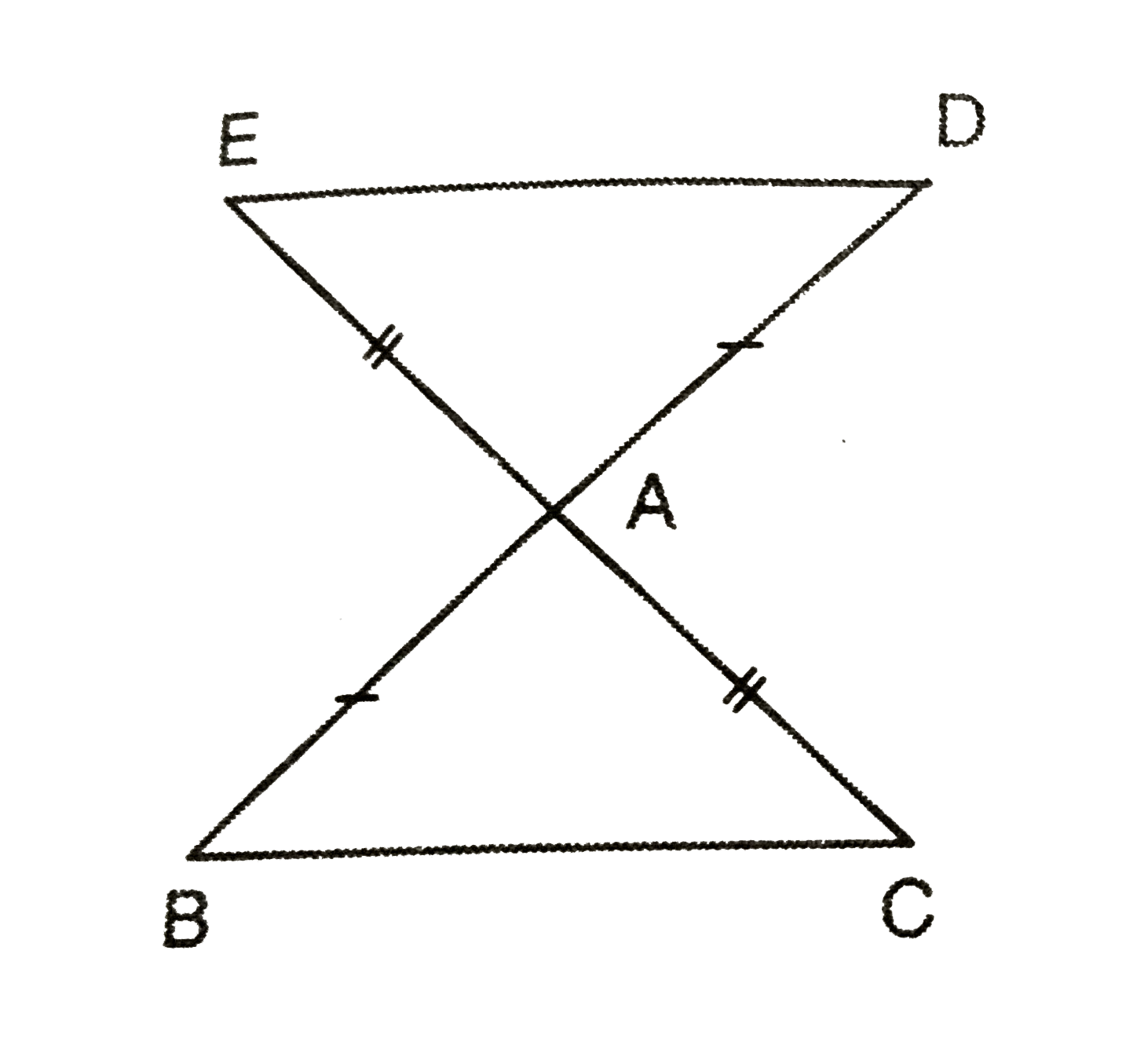
भुजाएँ BA तथा CA तथा इस प्रकार बढ़ाई गई कि BA=AD तथा CA=AE हैं | सिध्द कीजिए कि रेखाखण्ड DE∣∣BC है |
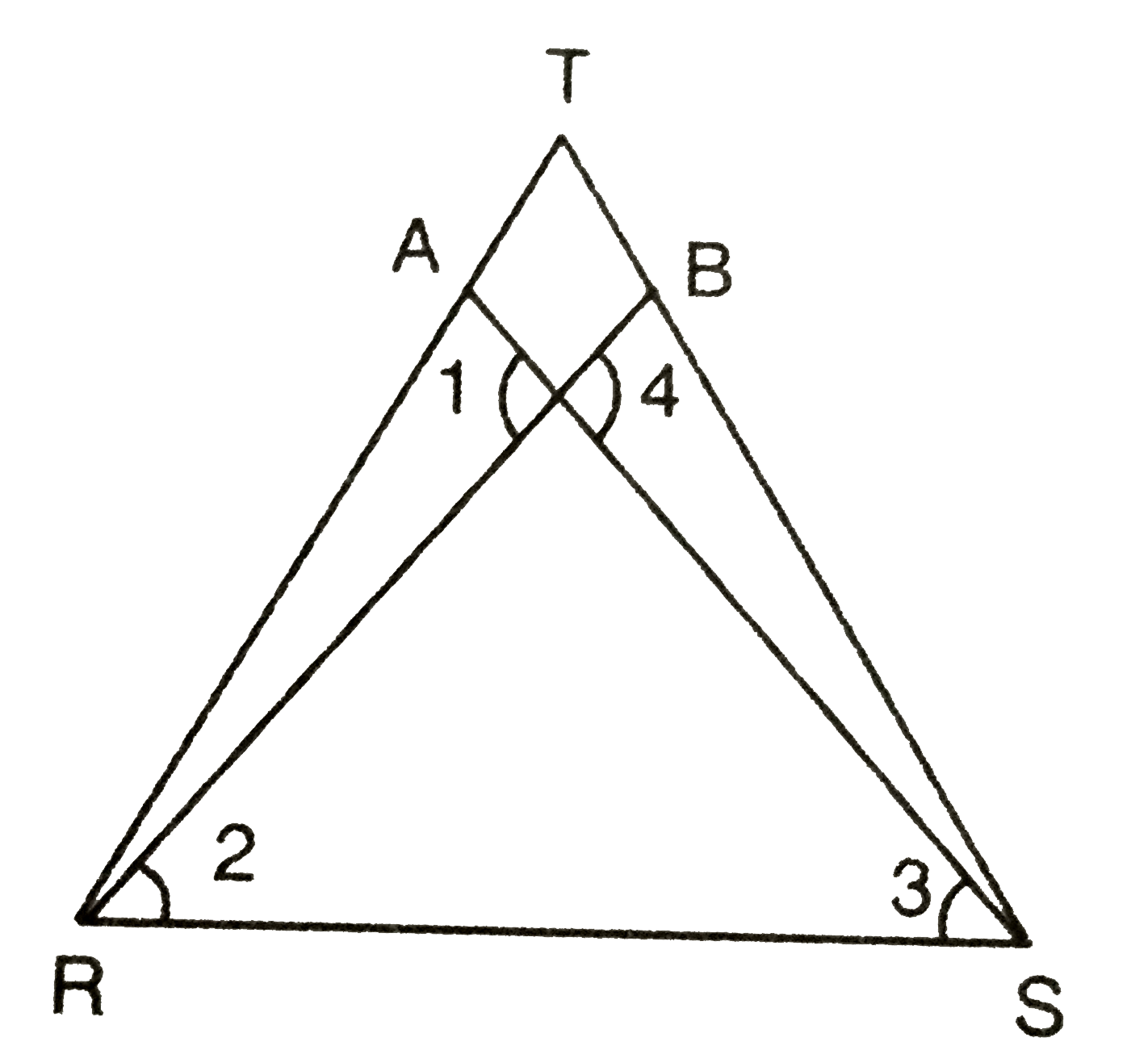
View Solutionयह दिया है RT=TS ∠1=2√3 तथा ∠4=2Sqrt(3)तो, दर्शाइए कि ΔRBT≅ΔSAT
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionप्रेक्षणो के सग्रह में से उच्चतम एव न्यूनतम प्रेक्षणो के अन्तर को कहते है ?
View SolutionIn the given figure, PS=PR,∠TPS=∠QPR. Prove that PT=PQ.
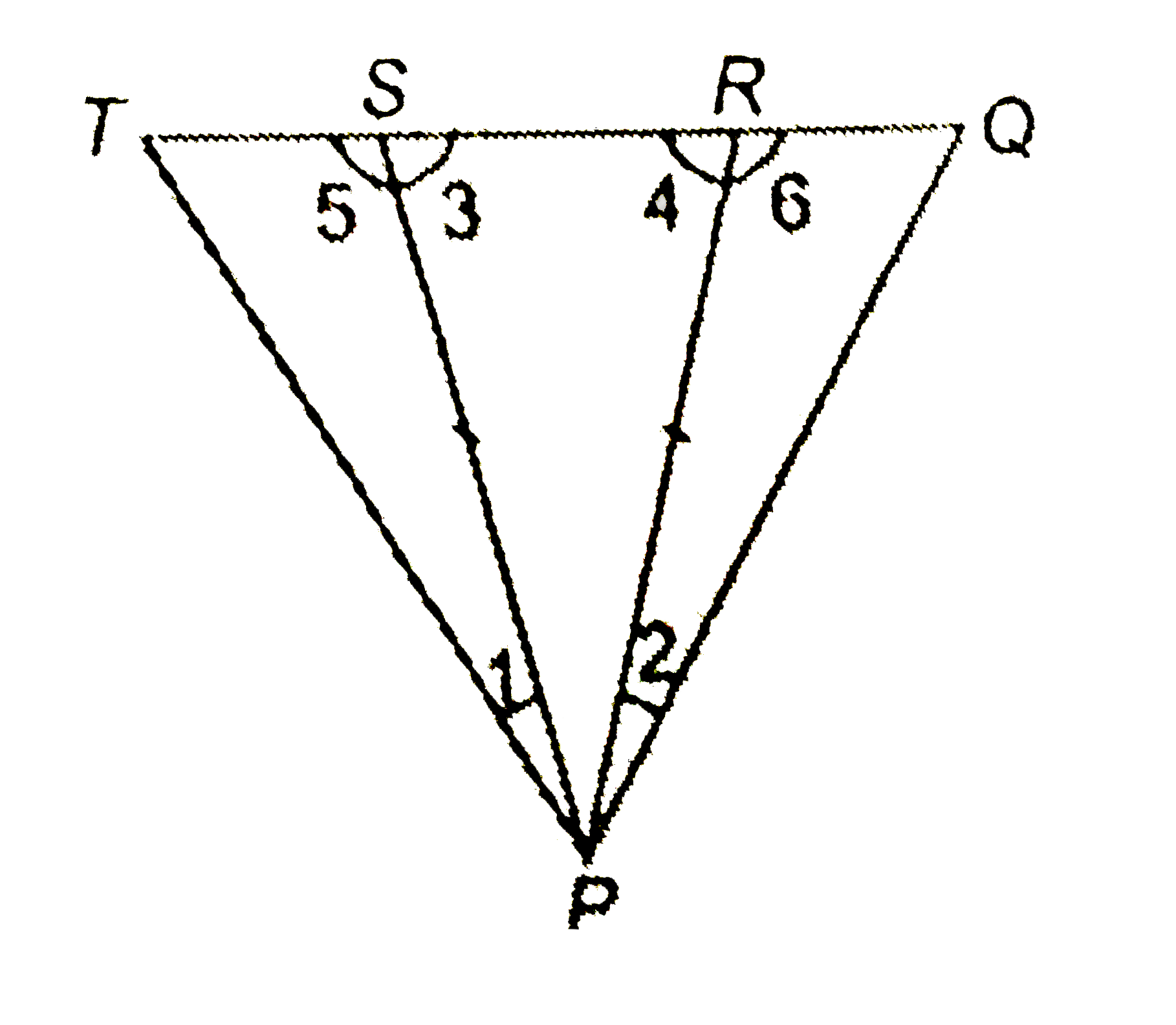
View Solutionनीचे के चित्र में PS=PR,∠TPS=∠QPR. साबित करें कि PT = PQ.
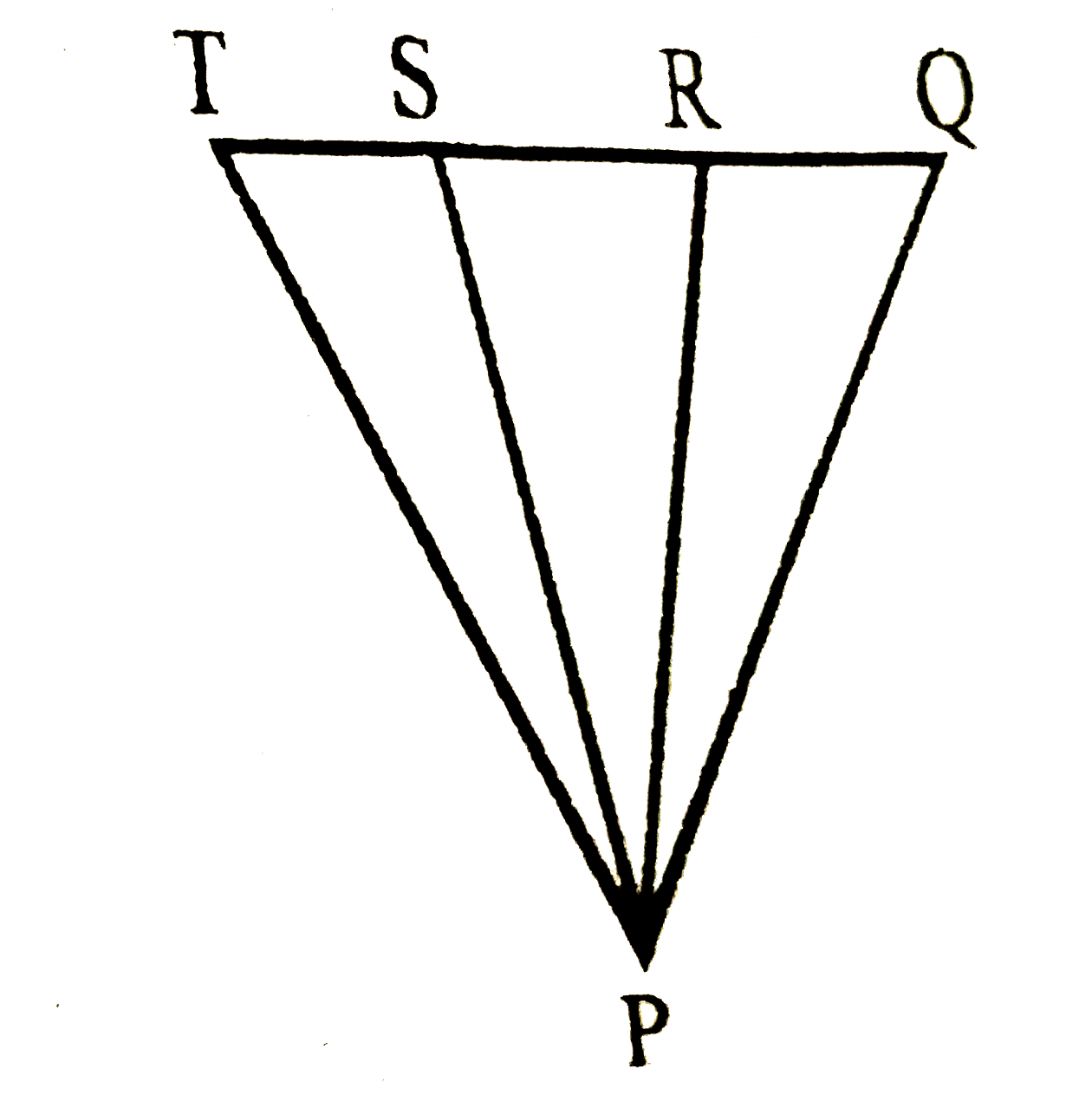
View Solutionयदि चतुर्भुज PQRS कि भुजाओं PS तथा RS पर क्रमशः T तथा U इस प्रकार हैं कि PQ=RQ, anglePQT=angleRQUतथाangleTQS=angleUQS तो, सिध्द करो कि QT=QU.
View Solutionमाना कि △PQR एक त्रिभुज है तथा →a=−−→QR,→b=−−→RP तथा →c=−−→PQ है | यदि |→a|=12,∣∣→b∣∣=4√3 तथा →b.→c=24 तो निम्न में से कोण-सा (से) सही है
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionयदि A सममित आव्यूह हो, तो सिद्ध करो कि M'AM भी सममित आव्यूह होगा|
View Solutionयदि z=(λ+3)+i√5−λ2 हो, तो सिध्द कीजिए कि z का बिन्दुपथ एक वृत्त होगा ।
View Solutionयदि a=cosθ+isinθ हो, तो सिध्द कीजिए कि 1+a1−a=i cotθ2
View Solutionयदि सम्मिश्र संख्याओं z, z + iz, iz से निरूपित बिन्दुओ से बनने वाले त्रिभुज का क्षेत्रफल 50 हो, तो सिध्द कीजिए कि |z|=10
View Solution

