यदि a+b=7 तथा ab = 12 हो , तो (a2−ab+b2) का मान ज्ञात कीजिए ।
हमे ज्ञात है कि :
a3+b3=(a+b)(a2−ab+b2)
उपरोक्त सर्वसमिका का उपयोग करने पर a2−ab+b2 का मान ज्ञात करने के लिए हमे (a3+b3) तथा (a+b) के मानो कि आवश्यकता होगी । चूँकि (a+b) का मान 7 दिया है इसलिए अब हम a3+b3 का मान ज्ञात करने का प्रयास करेंगे ।
हमे ज्ञात है कि :
a3+b3=(a+b)3−3ab(a+b)
⇒a3+b3=73−3×12×7 [a+b=7 तथा ab =12 रखने पर ]
⇒a3+b3=343−252=91
a+b तथा a3+b3 के मानो को सर्वसमिका ( i ) में रखने पर
91=7(a2−ab+b2)⇒917=(a2−ab+b2)⇒a2−ab+b2=13
वैकल्पिक विधि :
a2−ab+b2=a2+2ab+b2−2ab−ab
⇒a2−ab+b2=(a+b)2−3ab
⇒a2−ab+b2=72−3×12
⇒a2−ab+b2==49−36=13
Topper's Solved these Questions
- बीजीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - बीजीय सर्वसमिकाएँ EXERCISE - प्रश्नावली 4.1
28 Videos
- बीजीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - बीजीय सर्वसमिकाएँ EXERCISE - प्रश्नावली 4.2
23 Videos
- बीजीय व्यंजको का गुणनखण्डन BOOK - RD SHARMACHAPTER - बीजीय व्यंजको का गुणनखण्डन EXERCISE - बहु विकल्पीय प्रश्न
15 Videos
- यूक्लिड ज्यामिति - एक परिचयBOOK - RD SHARMACHAPTER - यूक्लिड ज्यामिति - एक परिचयEXERCISE - अति लघुत्तरात्मक प्रश्न
12 Videos
Similar Questions
सर्वसमिकाओ का उपयोग करके निम्नलिखित का मान ज्ञात कीजिये : ,
(2x−1x)2
View Solutionनिम्नलिखित को प्रसारित रूप में लिखिए :
(i) (a+2b+c)2
View Solutiona2−1−2x−x2 के गुणनखण्ड होंगे:
View Solutionएक रेखा को निरूपित करने के लिए कम से कम कितने बिदु की आवश्यकता होता है
View Solutionयदि बिंदु (1 ,-3 ) का स्थिति सदिश →a तथा →AB=→a एवं A का निर्देशांक (-1 ,5 ) हो तो B का निर्देशांक ज्ञात कीजिए||
View Solutionयदि 3+5r+7r2+……..∞=449 हो ,तो r का मान ज्ञात कीजिए ।
View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP का मान ज्ञात कीजिए।
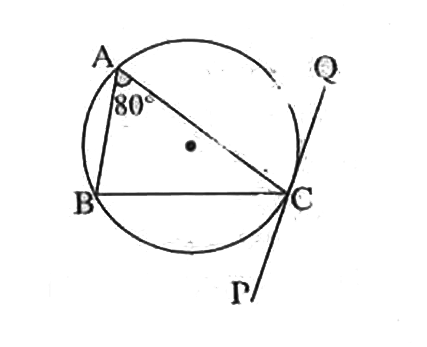
View Solutionयदि [a2+12b0b+3]=[2ab2+4b+102] तो a तथा b के मान ज्ञात कीजिए।
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=(2x−1)2+3
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=−(x−1)2+10
View Solution∣∣ ∣ ∣∣b2−abb−cbc−acab−a2a−bb2−abbc−acc−aab−a2∣∣ ∣ ∣∣ का मान ज्ञात कीजिए |
View Solutionयदि sin(A+B)=1 एवं cos(A-B)=1 हो, तो A तथा B का मान ज्ञात करे।
View SolutionIf A=0.142857142857.... and B=0.16666.... then what is the value of (A+B) /AB? यदि A=0.142857142857.... तथा B=0.16666.... है ,तो (A+B)/AB का मान क्या है?
View SolutionIf a^2+b^2+c^2=ab+bc+ac then the value of (a+c)/b is:- यदि a^2+b^2+c^2=ab+bc+ac हो, तो (a+c)/b का मान क्या होगा ?
View SolutionIf a^3-b^3=216 and a-b=6, then (a+b)^2 -ab is equal to: यदि a^3-b^3=216 तथा a-b=6, तो (a+b)^2 -ab का मान क्या होगा ?
View SolutionIf ab+bc+ca=8 and a+b+c=12 then (a2+b2+c2) is equal to:
यदि ab+bc+ca=8 तथा a+b+c=12 है, तो (a2+b2+c2) का मान ज्ञात करें |
View Solution
