आकृति में OPQR एक समचतुर्भुज है जिसके तीन शीर्ष O केन्द्र वाले वृत्त पर स्थित हैं । यदि समचतुर्भुज का क्षेत्रफल 32√3cm2 हो तो वृत्त की त्रिज्या ज्ञात करें

The correct Answer is:8 cm
माना की OQ और PR बिन्दु S पर काटते है |
स्पष्टत : PR⊥OQ
और OS=QS
माना की वृत्त की त्रिज्या = r
∴ OP=PQ=QR=OR=OQ=r
∴OS=r2
(##KCSHINMATIXC14E02010_S01.png width=80%><br>समकोणDeltaPSOमें<br> PS^(2) = OP^(2) - OS^(2)<br>" "=r ^(2) - ((r)/(2))^(2)<br> " "= r^(2) - (r^(2))/(4)) = (3r^(2))/(4)<br>therefore " "PS = sqrt(3r)/(2)<br>therefore " "PR = 2PS<br> = 2 xx (sqrt(3)r)/(2) = sqrt(3)r<br>अबसमचतुर्भुजPORQकाक्षेत्रफल= (1)/(2) xx PR xx OQ<br> therefore" " 32 sqrt(3) = (1)/(2) xx sqrt(3r) xxr<br>या, r = 64<br>therefore " " r = 8 cm
अतः वृत्त की त्रिज्या = 8 cm

Topper's Solved these Questions
- हीरोन का सूत्र BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - वस्तुनिष्ठ प्रश्न
13 Videos
- हीरोन का सूत्र BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - EXERCISE-14:1 (लघु उत्तरीय प्रश्न)
20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
Similar Questions
यदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View Solutionनिम्नलिखित त्रिभुजों का परिमाप एवं हीरो के सूत्र से क्षेत्रफल ज्ञात करें :
एक त्रिभुज जिसकी भुजाएँ 13 cm, 14 cm और 15 cm हैं ।
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
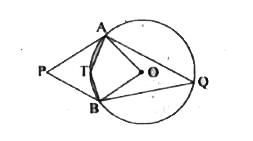
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
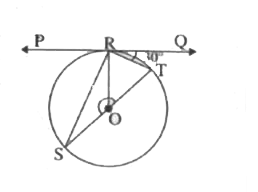
View Solutionआकृति में PQ ,Q केंद्र वाले वृत्त की स्पृह रेखा है जो वृत्त को R पर स्पर्श करती है। यदि कोण TRQ=30∘ हो तो ∠SOR एवं ∠RTO का मान ज्ञात कीजिए।
View Solution
