एक ताल निर्देशाक्षों से A, B, C पर इस प्रकार मिलता है कि ΔABC का केन्द्रक बिंदु (a,b,c) है | सिद्ध कीजिये कि तल का समीकरण xa+yb+zc=3 है |
माना कि तल की समीकरण है, xα+yβ+zγ=1 ...(1)
यदि तल x,y तथा z - अक्षो से क्रमशः A, B, C पर मिलता है तो A, B, C के निर्देशांक क्रमशः (α,0,0),(0,β,0) एवं (0,0,γ) होंगे |
इस प्रकार ΔABC के केन्द्रक (centroid ) के निर्देशांक (α3,β3,γ3) होंगे |
लेकिन दिया हुआ है कि ΔABC का केन्द्रक (a,b,c) है |
∴α3=a,β3=b,γ3=c
∴α=3a,β=3b,γ=3c.
अतः तल का अभीष्ट समीकरण है :
xa+yb+zc=3
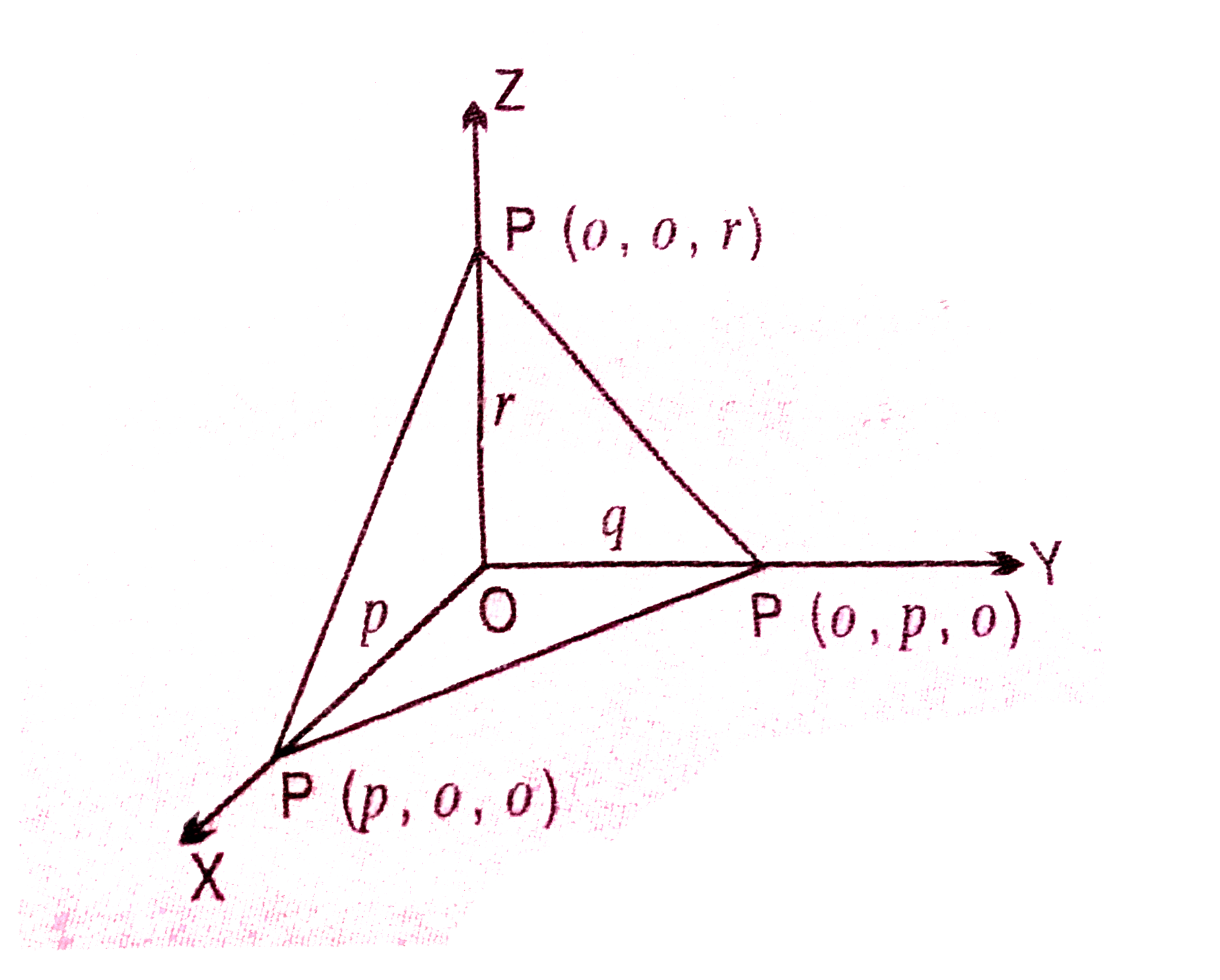
Topper's Solved these Questions
Similar Questions
इन तलों के कार्तीय समीकरण ज्ञात करें जिनके सदिश समीकरण है :
→r⋅(3ˆi+3ˆj−4ˆk)=0
View Solutionएक शंकु की ऊँचाई में वृद्धि 2% है तथा इसका अर्ध शीर्ष कोण अपरिवर्तित है। इसके (i) कुल पृष्ठ क्षेत्रफल (ii) आयतन में
सन्निकट प्रतिशत बढ़ोतरी वृद्धि क्या है?
View SolutionA के बारे में ज्ञात है कि वह 5 में से 3 बार सत्य बोलता है। वह एक पासे को फेंकता है और बतलाता है कि उस पर आनेवाली संख्या 1 है। इसकी प्रायिकता ज्ञात कीजिए कि पासे पर आने वाली संख्या वास्तव में 1 है।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionत्रिभुज ABC में कोण C समकोण है । यदि बिंदु A और B निर्देशांक क्रमशः (−3,4) और (3,−4)हो , तो सिद्ध कीजिये की ΔABC के परिवृत्त का समीकरण x2+y2=25 होगा ।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
View Solutionकिसी त्रिभुज ABC में A और B स्थिर बिंदु है । शीर्ष C इस प्रकार गमन करता है कि cotA+cotB=λ, जहाँ λ अचर है । C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु P का बिन्दुपथ ज्ञात कीजिए जो इस प्रकार गमन करता है कि बिंदु A(am,0),m≠1 से उसकी दूरी , बिंदु B(am,0) से उसकी दूरी की m गुनी रहती है ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु का बिन्दुपथ जो इस प्रकार गमन करता है कि बिंदु की दोनों अक्षों से दूरी सदैव समान रहती है ………… होगा ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solution
