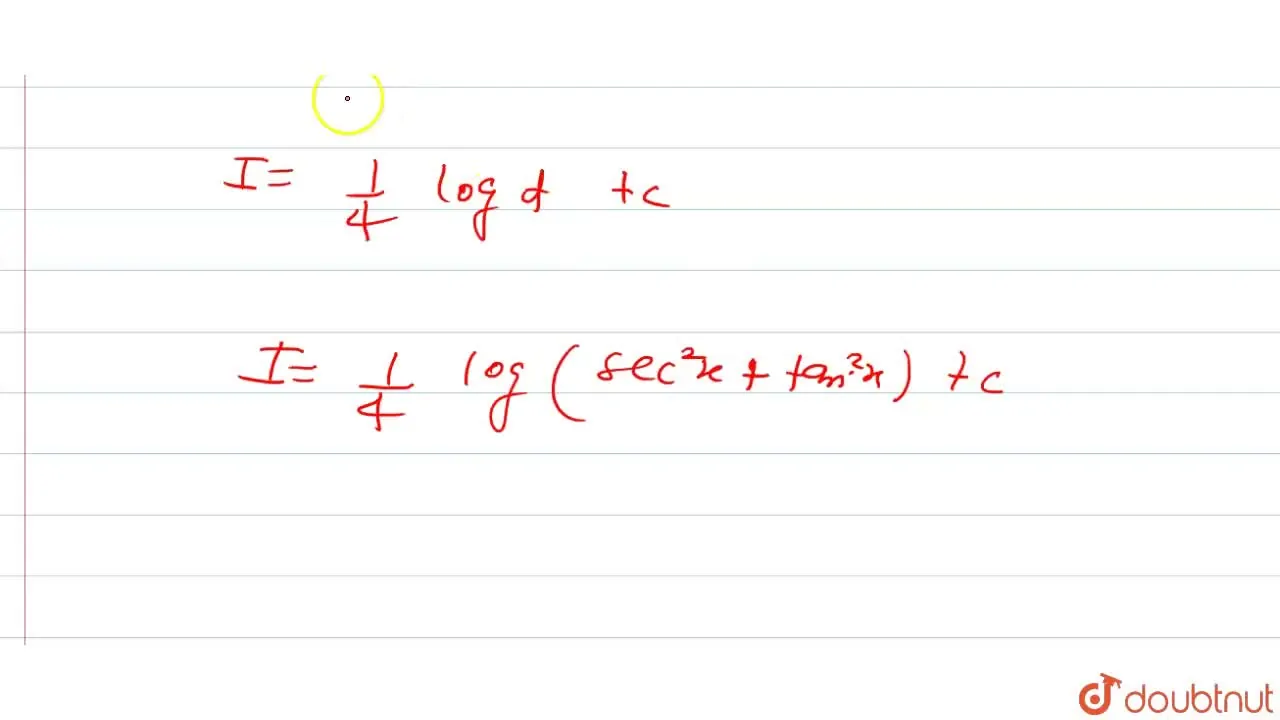ज्ञात करें ∫sec2xtanxsec2x+tan2xdx
Video Solution
Text Solution
z=sec2x+tan2x, रखे, तो
dz=(2 secx. secx tanx + 2 tanx sec2x)dx=4sec2xtanx dx
अब, I=I4∫dzz=14log|z|+c=14log(sec2x+tan2x)+c
|
Updated on:21/07/2023
Related Playlists
- BOOK - KC SINHACHAPTER - अनिश्चित समाकल EXERCISE - अभ्यास 19.149videos
अनिश्चित समाकल
- BOOK - KC SINHACHAPTER - अनिश्चित समाकल EXERCISE - अभ्यास 19.262videos
अनिश्चित समाकल
- BOOK - KC SINHACHAPTER - QUESTIONS OF J.A.C. 2014EXERCISE - SECTION-D10videos
QUESTIONS OF J.A.C. 2014
- BOOK - KC SINHACHAPTER - अवकल समीकरण EXERCISE - अभ्यास 23.745videos
अवकल समीकरण
Similar Questions
∫Cos2x
02:27View Solution∫dx√x+a−√x+2
01:56View Solutionसिद्ध करें कि 9π8−94sin−113=94sin−12√23
01:46View Solutionवैसे अवकल समीकरणों के हल पर आधारित प्रशन जिनको उपयुक्त प्रतिस्थापन द्वारा dy/dx+Py=Q , के रूप में लाया जा जहाँ P और Q केवल x के फलन या अचर हों: अवकल समीकरणों को हल करें| xdydx−3y=x2
03:36View SolutionEvaluate: ∫sec2xtanx+2dx
04:17View Solution∫(secx+tanx)2dx
02:45View Solutionint(sec^(2)x)/(log(tan x)^(tan x)dx)
03:00View Solutionint(sec x)/((sec x+tan x)^(2))dx
01:36View SolutionEvaluate: (i) ∫secxlog(secx+tanx) dx (ii) ∫cosec xlogtan(x2) dx
00:43View SolutionEvaluate: (i) ∫tanxsec2x(a+btan2x)2 dx (ii) ∫sec3xtanx dx
06:58View Solution∫sec2x√16+tan2xdx
00:43View Solution∫tanxsec2xdx
01:49View Solution∫sec(secx+tanx)dx.
01:24View Solution∫sec2x(secx+tanx)5dx=
03:30View Solution∫(sec2x)(2+tanx)dx
02:26View Solution