यंग के द्विस्लिट प्रयोग में फ्रिंज चौड़ाई के लिए व्यंजक व्युत्पन्न कीजिये।
मान लो S एक स्लिट है जो एकवर्णी प्रकाश स्त्रोत से प्रकाशित है । और एक - दूसरे के समीप दो स्लिटें है जो S के समान्तर हैं तथा S के समान्तर हैं तथा S से बराबर दूरी पर स्थित हैं । अतः और दो कला - संबद्ध स्त्रोत की तरह कार्य करेंगे ।
मान लो
मान लो दोनों स्त्रोतों से D दूरी पर एक पर्दा XY हैं , जिस पर व्यतिकरण फ्रिंजें बनती हैं ।
पर्दे पर बिंदु दोनों स्त्रोतों से बराबर दूरी पर हैं । अतः इस बिंदु पर दोनों स्त्रोतों से चलकर पहुँचने वाली तरंगों के मध्य पथांतर शून्य होगा । फलस्वरुप बिंदु पर तीव्रता अधिकतम होगी ।
मान लो पर्दे पर बिंदु से x दूरी पर एक बिंदु P हैं । से पर्दे XY पर लम्ब डालो । मान लो का मध्य बिंदु O हैं । तब S, O और एक ही रेखा पर होंगे ।
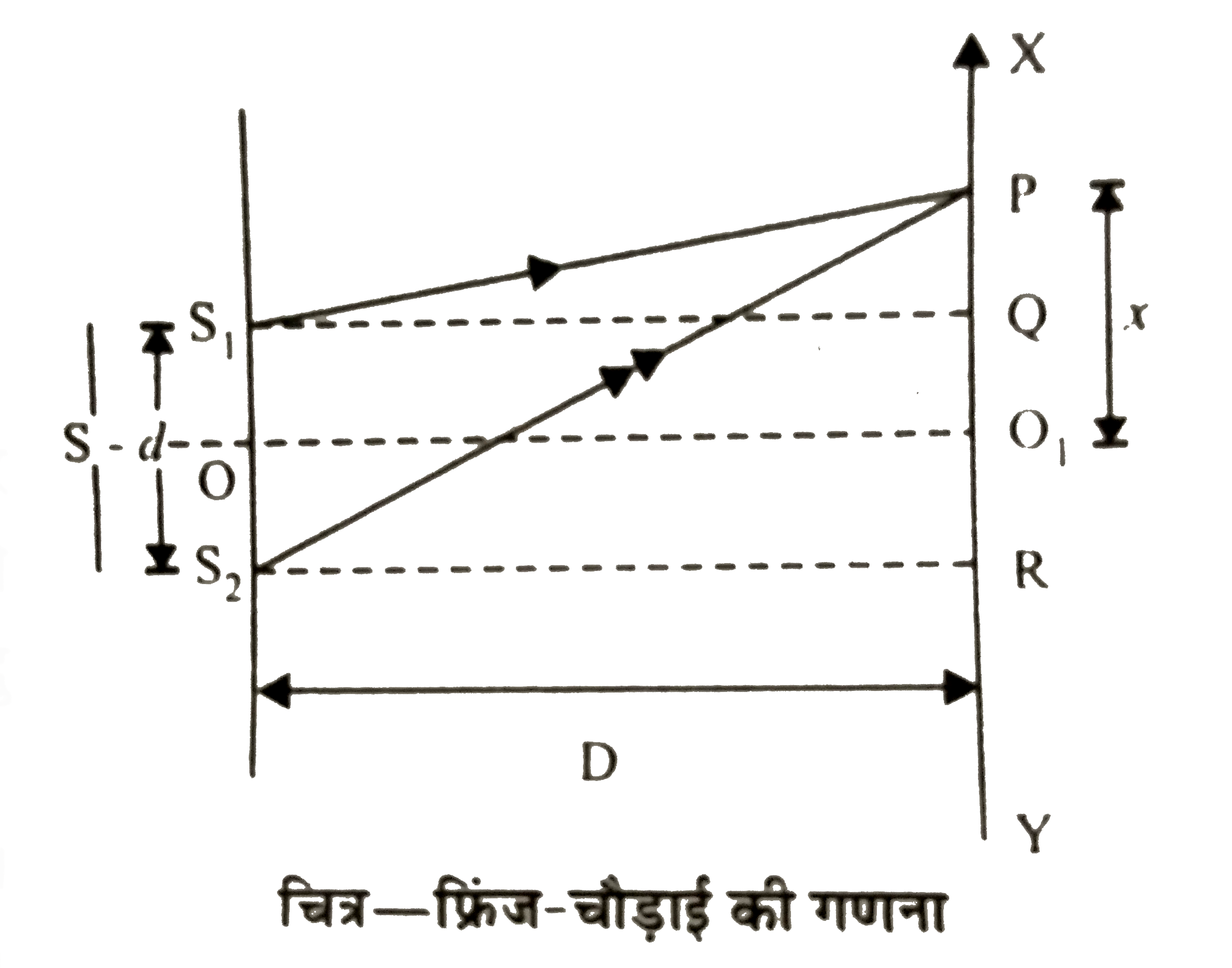
समकोण में
इसी तरह समकोण में ,
या
या = 2 xd
या
परंतु (लगभग ) (क्योंकि व्यवहार में बिंदु P बिंदु के अत्यंत निकट होता हैं ।)
अर्थात् पथान्तर
(i) दीप्त फ्रिन्जें (Bright Fringes) - अधिकतम तीव्रता के लिए व्यतिकरण करने वाली तरंगों के मध्य पथान्तर का समगुणक होता हैं ।
या
...(2)
जहाँ n = 0,1,2,3,....
समीकरण (2) में n = 0 रखने पर केंद्रीय दीप्त फ्रिन्ज की स्थिति प्राप्त होती हैं । इसे शून्य क्रम फ्रिंज कहते हैं ।
n = 1,2,3,.... रखने पर क्रमशः प्रथम , व्दितीय , तृतीय , ...... दीप्त फ्रिंजों की स्थितियाँ प्राप्त होती हैं ।
(ii) अदीप्त फ्रिंजें (Dark Fringes) - न्यूनतम तीव्रता के लिए व्यतिकरण करने वाली तरंगों के मध्य पथान्तर का विषम गुणक होता हैं ।
पथांतर (जहाँ n = 1,2,3....)
या .....(3)
अतः दो क्रमागत दीप्त फ्रिंजों के बीच की दूरी अर्थात् अदीप्त फ्रिंज की चौड़ाई ,
...(4)
इस तरह यदि केंद्रीय फ्रिंज O से nवीं और (n + 1) वीं अदीप्त फ्रिंजों की दूरियों क्रमशः हों , तो
तथा
अतः दो क्रमागत अदीप्त फ्रिंजो के बीच की दूरी अर्थात् दीप्त फ्रिंज की चौड़ाई ,
...(5)
समी. (4) और (5) से स्पष्ट है कि दीप्त और अदीप्त फ्रिंजों की चौड़ाई एकसमान होती हैं ।
इस तरह फ्रिंज चौड़ाई . यही अभीष्ट व्यंजक हैं ।
Topper's Solved these Questions
- तरंग प्रकाशिकी Book:NAVBODHChapter:तरंग प्रकाशिकी Exercise:आंकिक प्रश्न
Explore 44 Videos
- तरंग प्रकाशिकी Book:NAVBODHChapter:तरंग प्रकाशिकी Exercise:उदाहरण
Explore 3 Videos
- तरंग प्रकाशिकी Book:NAVBODHChapter:तरंग प्रकाशिकी Exercise:लघु उत्तरीय प्रश्न
Explore 77 Videos
- चुंबकत्व और द्रव्य Book:NAVBODHChapter:चुंबकत्व और द्रव्य Exercise:आंकिक प्रश्न
Explore 15 Videos
- तरलो के यांत्रिक गुण- IIBook:NAVBODHChapter:तरलो के यांत्रिक गुण- IIExercise:बहुविकल्पीय प्रश्न
Explore 30 Videos
Similar Questions
वायु से काँच में संक्रमण के लिए ब्रुस्टर कोण क्या हैं ? (काँच का अपवर्तनांक 1⋅5)
View Solutionयंग के द्वीसिल्ट प्रयोग में न्यूनतम तीव्रता एवं अधिकतम तीव्रता का अनुपात 9:25 है | दोनों स्लिटों की चौडाईयाँ का अनुपात ज्ञात कीजिये |
View Solutionतरंगों के अध्यारोपण का सिद्धांत क्या है ?
View Solutionएक चुम्बकीय तार का चुम्बकीय आघूर्ण M है। उसे एक सिरे से एक तिहाई दूरी पर लंबवत L आकार में मोड़ दिया जाता है । अब उसका नया चुंबकीय आघूर्ण कितना हो जायेगा ?
View Solutionकिसी नलिका से बहने वाले द्रव का क्रांतिक वेग की विमाओ को (ηx,ρyrz)से निर्दिष्ट किया जाता है , जहाँ η,ρतथा r क्रमशःद्रव का श्यानता गुणांक , द्रव का घनत्व तथा नली की त्रिज्या है । x,y,zके मान क्रमशःहोंगे -
View Solutionइन आव्यूहों के सहखंडाज आव्यूह कीजिये -
[αβγδ]
उपयुक्त आव्यूहों के लिए (adj. A)A=|A|I=A(adj.A) सत्यापित कीजिये।
View Solutionयंग का प्रयोग
View Solutionयंग का द्वि- स्लिट प्रयोग#!#यंग का एकल झिरी प्रयोग
View Solutionगरुभूमि के इलाके में वर्षा की मात्रा नापने के लिए किस इकाई.का प्रयोग होता है?
View Solutionबच्चों में भाषा प्रयोग की दक्षता विकसित करने के लिए आवश्यक है
View Solutionभाषा में आकलन का प्रयोग मुख्यतः …………….. के लिए होना चाहिए।
View Solutionनाइट्रोजन (III) के व्युत्पन्न किस रूप में कार्य करते हैं?
View Solutionपौधों में सेलुलोस, पशुओं के लिए खाद्य के रूप में उपस्थित होता है, लेकिन इंसानों के लिए नहीं क्योंकि:
View Solutionकेप्रोलेक्टम का प्रयोग किसके विनिर्माण के लिए किया जाता है?
View Solutionअनेक शब्दों के लिए एक शब्द और उनका प्रयोग
View Solutionआकलन का प्रयोग _______ के लिए होना चाहिए।
View Solution

