Triangle ABC has AC=13,AB=15andBC=14. Let 'O' be the circumcentre of the ΔABC. If the length of perpendicular from the point 'O' on BC can be expressed as a rational mn in the lowest form then find (m+n).
The correct Answer is:m+n=33+8=41.
Step by step video, text & image solution for Triangle ABC has AC=13, AB = 15 and BC = 14. Let 'O' be the circumcentre of the DeltaABC. If the length of perpendicular from the point 'O' on BC can be expressed as a rational m/n in the lowest form then find (m +n). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise For Sesssion 1
Explore 20 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise For Sesssion 2
Explore 19 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 52 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
Triangle ABC has AC=13,AB=15 and BC=14. Let Obe the circumcentre of the A B C.Ifthe≤n>hofperpendica––romthep∮'O'onB Ccanbeexpressedasarationalm/n∈thelowestformthenf∈d(m+n).
View SolutionIn △ABC , AB=10
AC=7,BC=9
then find the length find the length of the median drawn from point C to side AB .
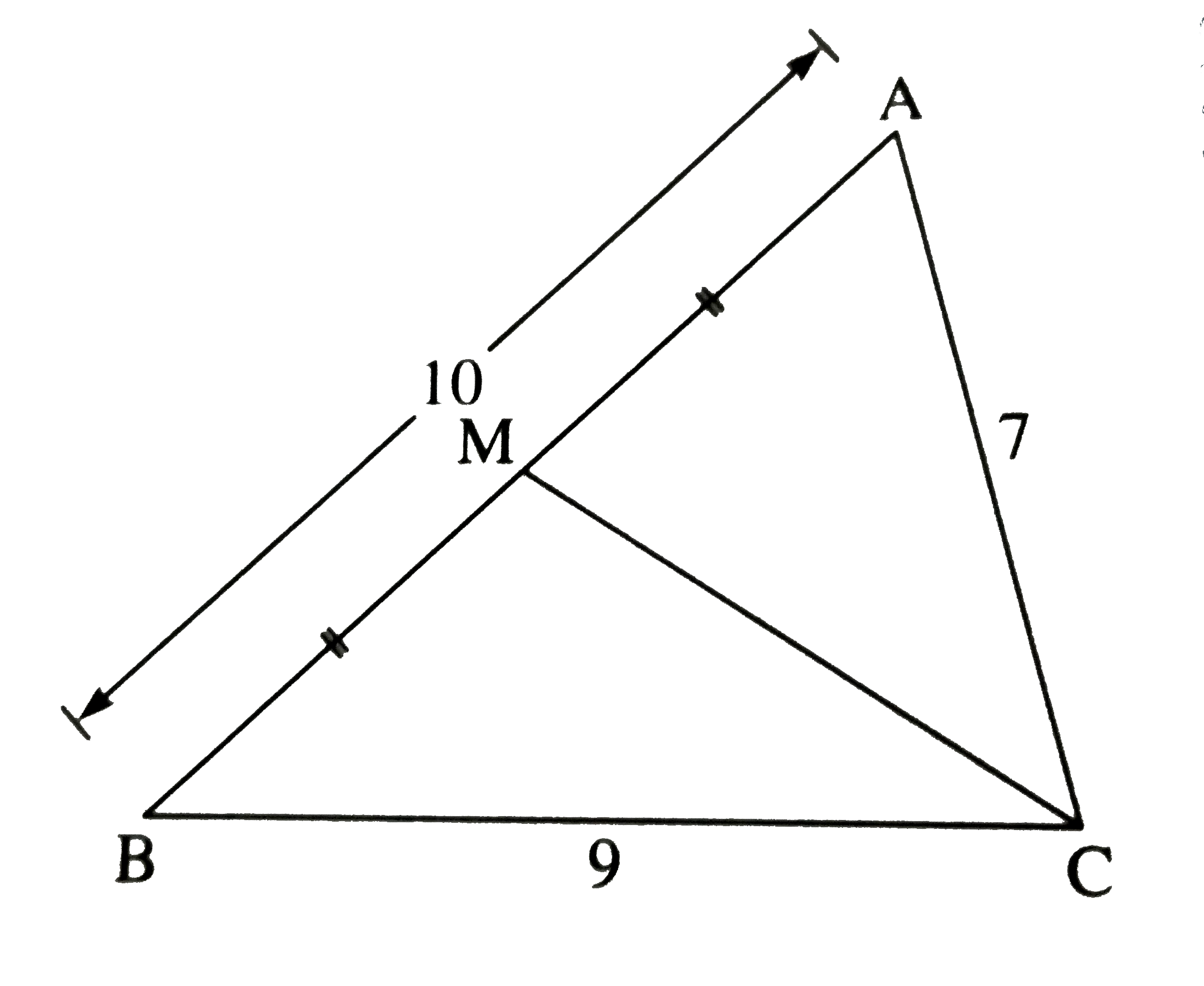
View Solution
Knowledge Check
In a △ABC,AB = 10 cm, BC = 12 cm and AC = 14 cm. Find the length of median AD. If G is the centroid, find length of GA.
A53√7,59√7B5√7,4√7C10√3,83√7D4√7,83√7The diagonal of the square field measures 50m. The area of square field is?
Aa. 1250m^2Bb. 1200m^2Cc. 1205m^2Dd. 1025m^2O is the circumcentre of a triangle ΔABC. The point A and the chord BC are on the opposite side of O. If ∠BOC=150∘. Then the angle ∠BACis :
A65∘B60∘C70∘D75∘
In a ΔABC AB = 13 , BC = 14 , CA = 15 find the radius of excentre .
View SolutionO is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
View SolutionIn ΔABC, AB=10, AC=7, BC=9, then find the length of the median drawn from point Cto side AB.
View SolutionIn triangle ABC,BC=8 cm, AC=15 cm and AB=17 cm. The length of the altitude drawn from B on AC is :
View SolutionO is the circumcentre of a triangle ΔABC.The point A and the chord BC are on the opposite side of O.If ∠BOC=150∘.Then the angle ∠BAC is:
View Solution