Consider f:(0,∞)→(−π2,π2), defined as f(x)=tan−1(logex(logex)2+1). The about function can be classified as

A

Injective but nor surjective

B

Surjective but not bijective

C

Neither injective nor surjective

D

Both injective and surjective

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for Consider f:(0, oo)->(-pi/2,pi/2), defined as f(x) = tan^-1 (log_e x/((log_e x)^2+1)). The about function can be classified as by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSDEFINITE INTEGRAL

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
    The above function can be classified as :

    Ainjective but not surjective
    Bsurjective but not injective
    Cneither injective nor surjective
    Dboth injective as well as surjective

  • f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
    The graph of y = f (x) is best represented by

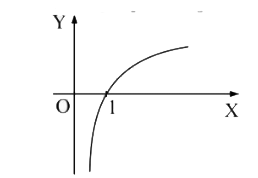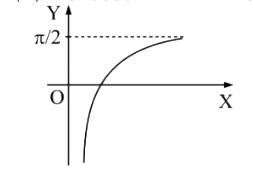    Aocr_image
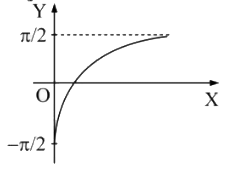    Bocr_image
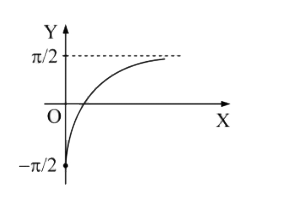
    Cocr_image
    Docr_image

  • f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
    If x1,x2andx3 are the points at which g(x) =[f (x)] is discontinuous (where, [.] denotes the greatest integer function), then (x1+x2+x3) is :

    A2
    B3
    Cgreater than 3
    Dbelong to