To find the point of contact P(x1,y1) of a tangent to the graph of y=f(x) passing through origin O, we equate the slope of tangent to y=f(x) at P to the slope of OP. Hence we solve the equation f'(x)=f(x1)x1 to get x1 and y1.Now answer the following questions (7 -9): The equation |lnmx|=px where m is a positive constant has a single root for
p<me
0<p<me
0<p<em
p<em
The correct Answer is:B
Step by step video, text & image solution for To find the point of contact P (x_1, y_1) of a tangent to the graph of y = f(x) passing through origin O, we equate the slope of tangent to y = f(x) at P to the slope of OP. Hence we solve the equation f' (x) = f(x_1)/x_1 to get x_1 and y_1.Now answer the following questions (7 -9): The equation |lnmx|= px where m is a positive constant has a single root for by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHSChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise (Matching Type Questions)
Explore 1 Video
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHSChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise (Single Integer Answer Type Questions)
Explore 9 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHSChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise (Statement I And Ii Type Questions)
Explore 7 Videos
- DIFFERENTIATION Book:ARIHANT MATHSChapter:DIFFERENTIATION Exercise:Exercise For Session 10
Explore 4 Videos
- ELLIPSEBook:ARIHANT MATHSChapter:ELLIPSEExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 27 Videos
Similar Questions
Knowledge Check
To find the point of contact P≡(x1,y1) of a tangent to the graph of y=f(x) passing through origin O, we equate the slope of tangent to y=f(x) at P to the slope of OP. Hence we solve the equation f'(x1)=f(x1)x1 to get x1andy1.
The equation |lnmx|=px where m is a positive constant has a single root forA0<p<m/eBp<e/mC0<p<e/mDp>m/eA curve y=f(x) is passing through (0,0). If slope of the curve at any point (x,y) is equal to (x+xy), then the number of solution of the equation f(x)=1, is :
A0B1C2D4
Determine the equation of the curve passing through the origin , the slope of the tangent of which at any point(x,y) is x+1y+1 .
View SolutionThe graph of the function y=f(x) is shown.
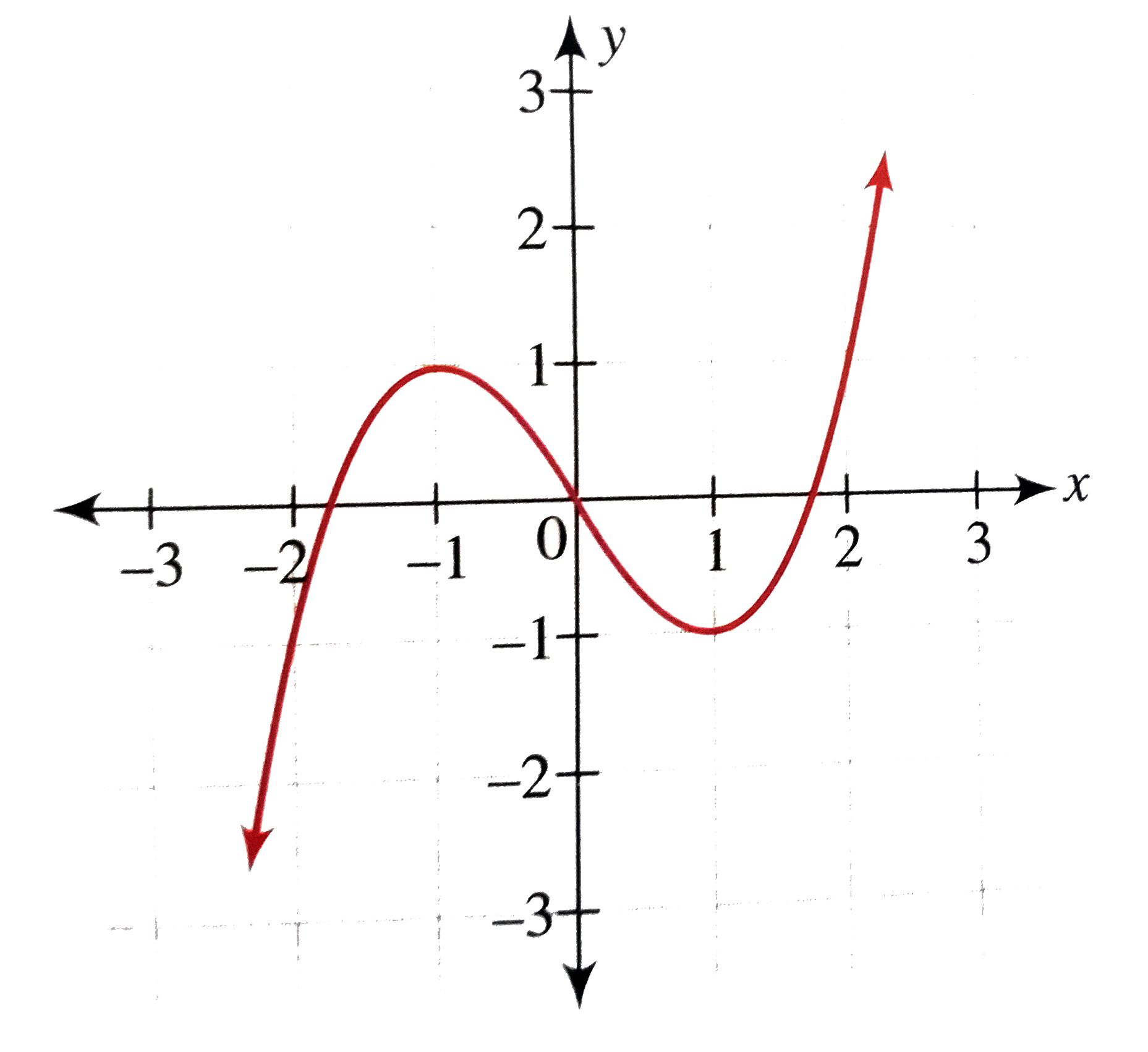
Find the number of solutions to the equation ||f(x)|−1|=12.
View SolutionFind the equation of the cure which passes through the origin and has the slope x+3y−1 at the point (x,y) on it.
View SolutionThe length of tangent at a point P(x1,y1) to the curve y=f(x) ,having slope m at P is
View SolutionIf f'(x)=x−1, the equation of a curve y=f(x) passing through the point (1, 0) is given by
View SolutionEquation of the tangent to y2=4a(x+a) having slope 1 is
View Solution

