A air-foce plane is ascending vertically at the rate of 100 km/h. If the radius of the earth is r km, how fast is the area of the earth, visible from the plane, increasing at 3 min after it started ascending?
Note Visible area A=2πr2hr+h, where h is the height of the plane above the earth.
The correct Answer is:200π3(r+5)2km2/h
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the Formula for Visible Area
The visible area A of the Earth from the plane is given by the formula:
A=2πr2hr+h
where r is the radius of the Earth and h is the height of the plane above the Earth's surface.
Step 2: Differentiate the Area with Respect to Time
We need to find how fast the area A is increasing, which means we need to differentiate A with respect to time t:
dAdt=ddt(2πr2hr+h)
Using the quotient rule, we differentiate:
dAdt=2πr2⋅(r+h)dhdt−hddt(r+h)(r+h)2
Since r is constant (the radius of the Earth), drdt=0.
Step 3: Simplify the Derivative
Substituting drdt=0 into the equation gives:
dAdt=2πr2((r+h)dhdt−h⋅0)(r+h)2
This simplifies to:
dAdt=2πr2(r+h)dhdt(r+h)2
Step 4: Calculate Height h After 3 Minutes
The plane ascends at a rate of 100 km/h. After 3 minutes, we convert minutes to hours:
3 minutes=360 hours=120 hours
Now, calculate h:
h=speed×time=100 km/h×120 h=5 km
Step 5: Substitute Values into the Derivative
Now we substitute h=5 km and dhdt=100 km/h into the derivative:
dAdt=2πr2(r+5)⋅100(r+5)2
This simplifies to:
dAdt=200πr2r+5
Final Step: Conclusion
Thus, the rate at which the area of the Earth visible from the plane is increasing at 3 minutes after it started ascending is:
dAdt=200πr2r+5 km2/h
The visible area A of the Earth from the plane is given by the formula:
A=2πr2hr+h
where r is the radius of the Earth and h is the height of the plane above the Earth's surface.
We need to find how fast the area A is increasing, which means we need to differentiate A with respect to time t:
dAdt=ddt(2πr2hr+h)
Using the quotient rule, we differentiate:
dAdt=2πr2⋅(r+h)dhdt−hddt(r+h)(r+h)2
Since r is constant (the radius of the Earth), drdt=0.
Substituting drdt=0 into the equation gives:
dAdt=2πr2((r+h)dhdt−h⋅0)(r+h)2
This simplifies to:
dAdt=2πr2(r+h)dhdt(r+h)2
The plane ascends at a rate of 100 km/h. After 3 minutes, we convert minutes to hours:
3 minutes=360 hours=120 hours
Now, calculate h:
h=speed×time=100 km/h×120 h=5 km
Now we substitute h=5 km and dhdt=100 km/h into the derivative:
dAdt=2πr2(r+5)⋅100(r+5)2
This simplifies to:
dAdt=200πr2r+5
Thus, the rate at which the area of the Earth visible from the plane is increasing at 3 minutes after it started ascending is:
dAdt=200πr2r+5 km2/h
Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHSChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise For Session 2
Explore 6 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHSChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise For Session 3
Explore 10 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHSChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 7 Videos
- DIFFERENTIATION Book:ARIHANT MATHSChapter:DIFFERENTIATION Exercise:Exercise For Session 10
Explore 4 Videos
- ELLIPSEBook:ARIHANT MATHSChapter:ELLIPSEExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 27 Videos
Similar Questions
An airforce plane is ascending vertically at the rate of 100 km/h. If the radius of the earth is rkm, how fast is the area of the earth, visible from the plane, increasing at 3 minutes after it started ascending? Given that the visible area A at height h is given by A=2πr2hr+h .
View SolutionA geostationary satellite is nearly at a height of h = 6 R from the surface of the earth where R is the radius of the earth. Calculate the area on the surface of the earth in which the communication can be made using this satellite.
View Solution
Knowledge Check
A geostationary satellite is at a height h above the surface of earth. If earth radius is R-
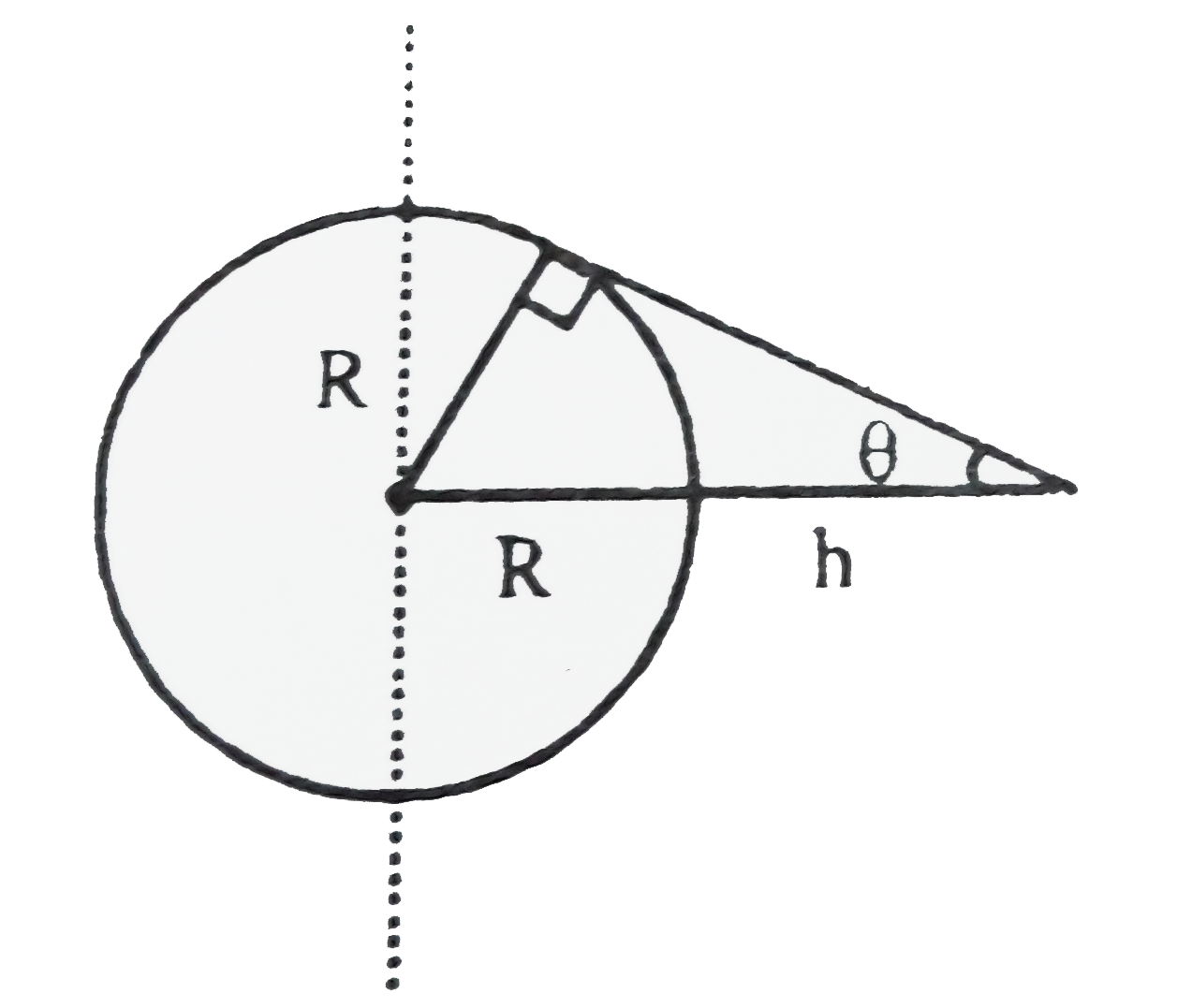 AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)
AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)A body of mass m is kept at a small height h above the ground. If the radius of the earth is R and its mass is M, the potential energy of the body and earth system (with h=∞ being the reference position) is
AGMmR+mghB−GMmR+mghCGMmR−mghD−GMmR−mghA rocket is launched vertically from the surface of the earth with an initial velocity v. How far above the surface of earth will it go? Neglect the air resistance. (where R is the radius of the earth )
AR(2gRv2−1)−1/2BR(2gRv2−1)CR(2gRv2−1)−1DR(2gRv2−1)2
The orbital velocity of a satellite is given by the expression V=sqrt((GM)/(R + h)), here M is the mass of the Earth, R is the radius of the Earth and 'h' is the height of the satellite from the surface of the Earth. Explain the reasons why the geostationary satellite is not possible to set in orbit around the Earth at two different heights from the surface of the Earth.
View SolutionAt what height h above the earth's surface, the value of g becomes g/2 (where R is the radius of the earth)
View SolutionThe value of gravitational accelerationg at a height h above the earth's surface is then (R = radius of earth)
View SolutionA cosmonaut is orbiting the earth in a spacecraft at an altitude h =630km with a speed of 8kms−2. If the radius of the earth is 6400km, the acceleration of the cosmonaut is
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. What is the time period of another satellite orbiting at a height of 2.5 R from the surface of the earth ?
View Solution

