Let F(x) be an indefinite integral of sin2x
Statement-1: The function F(x) satisfies F(x+π)=F(x) for all real x. because
Statement-2: sin3(x+π)=sin2x for all real x.
A) Statement-1: True , statement-2 is true, Statement -2 is not a correct explanation for statement -1
c) Statement-1 is True, Statement -2 is False.
D) Statement-1 is False, Statement-2 is True.
Statement I is true, Statement II is also true, Statement II is the correct explanation of Statement I.
Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I.
Statement I is true, Statement II is false.
Statement is false, Statement II is true.
The correct Answer is:D
Step by step video, text & image solution for Let F(x) be an indefinite integral of sin^(2)x Statement-1: The function F(x) satisfies F(x+pi)=F(x) for all real x. because Statement-2: sin^(3)(x+pi)=sin^(2)x for all real x. A) Statement-1: True , statement-2 is true, Statement -2 is not a correct explanation for statement -1 c) Statement-1 is True, Statement -2 is False. D) Statement-1 is False, Statement-2 is True. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - FUNCTIONSEXERCISE - Exercise (Subjective Type Questions)13videos
FUNCTIONS
- BOOK - ARIHANT MATHSCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)3videos
ESSENTIAL MATHEMATICAL TOOLS
- BOOK - ARIHANT MATHSCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)10videos
GRAPHICAL TRANSFORMATIONS
Similar Questions
Let F(x) be an indefinite integral of sin2x.
Statement- 1: The function F(x) satisfies F(x+π)=F(x) for all real x.
Statement- 2: sin2(x+π)=sin2x for all real x.
(A) Statement I is true, Statement II is also true, Statement II is the correct explanation of Statement I.
(B)Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I.
(C) Statement I is true, Statement II is false.
(D) Statement I is false, Statement II is ture.View SolutionConsider the function F(x)=∫x(x−1)(x2+1)dxStatement-1: F(x) is discontinuous at x=1 ,Statement-2: Integrand of F(x) is discontinuous at x=1 (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View Solution
Knowledge Check
- Question 1 - Select One
Let F(x) be an indefinite integral of sin2x Statement I The function F(x) satisfies F(x+π)=F(x) for all real x. Because Statement II sin2(x+π)=sin2x, for all real x. (A) Statement I is true, Statement II is also true,
Statement II is the correct explanation of Statement I. (B)Statement I is true, Statement II is also true,
Statement II is not the correct explanation of Statement I. (C) Statement I is true, Statement II is false. (D) Statement I is false, Statement II is ture.AStatement I is true, Statement II is also true,
Statement II is the correct explanation of Statement I.BStatement I is true, Statement II is also true,
Statement II is not the correct explanation of Statement I.CStatement I is true, Statement II is false.DStatement I is false, Statement II is ture.
Statement-1: The function F(x)=∫sin2xdx satisfies F(x+π)=F(x),∀ξnR ,Statement-2: sin2(x+π)=sin2x (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionLet f: R R be a continuous function defined by f(x)=1ex+2e−x . Statement-1: f(c)=13, for some c∈R . Statement-2: 0<f(x)≤12√2, for all x∈R . (1) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation for Statement-1 (2) Statement-1 is true, Statement-2 is false (3) Statement-1 is false, Statement-2 is true (4) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation for Statement-1
View SolutionStatement-1: ∫sin−1xdx+∫sin−1√1−x2dx=π2x+cStatement-2: sin−1x+cos−1x=π2 (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: Yield of R-Br follows the order 1∘>2∘>3∘ in Hundsdicker reaction
Statement -2: Hundsdicker reaction follows free redical mechanism.View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: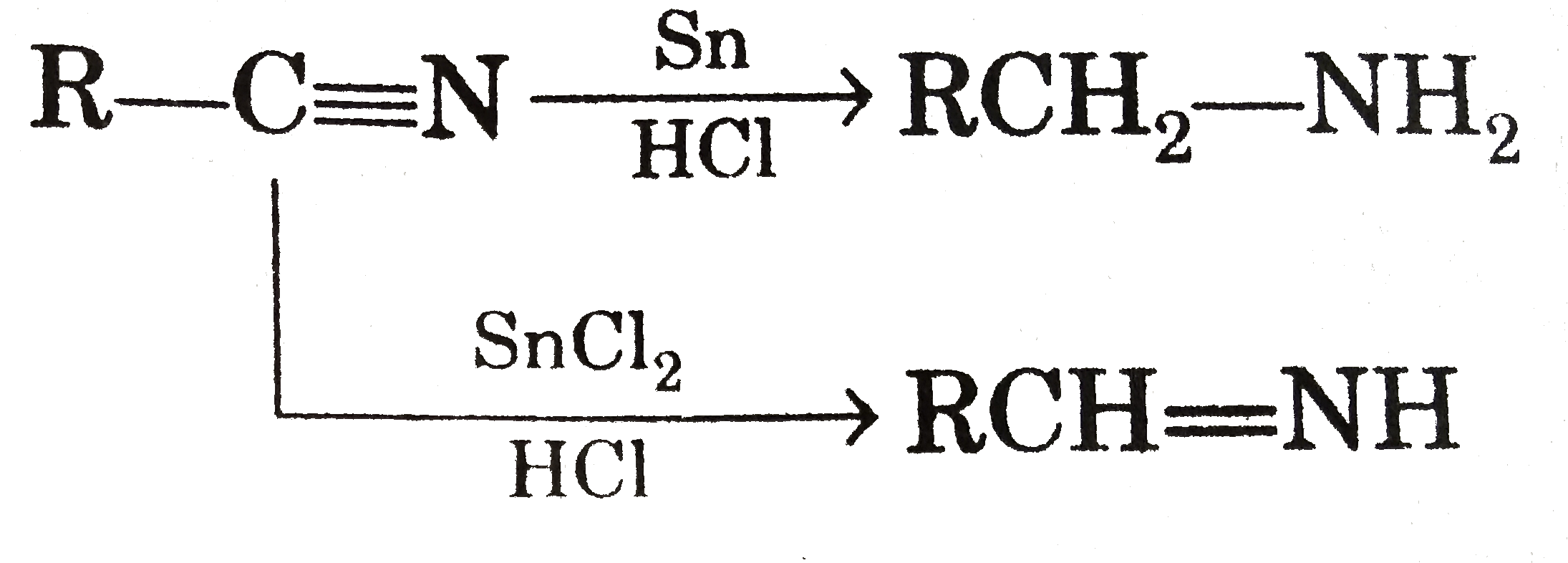
Statement-2: Sn can give maximum of 4 electron during reduction, whereas SnCl2 can give only 2.View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: Effective molecular mass of acetic acid is 120.
Statement -2: It forms dimer due to intramolecular H-bonding.View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: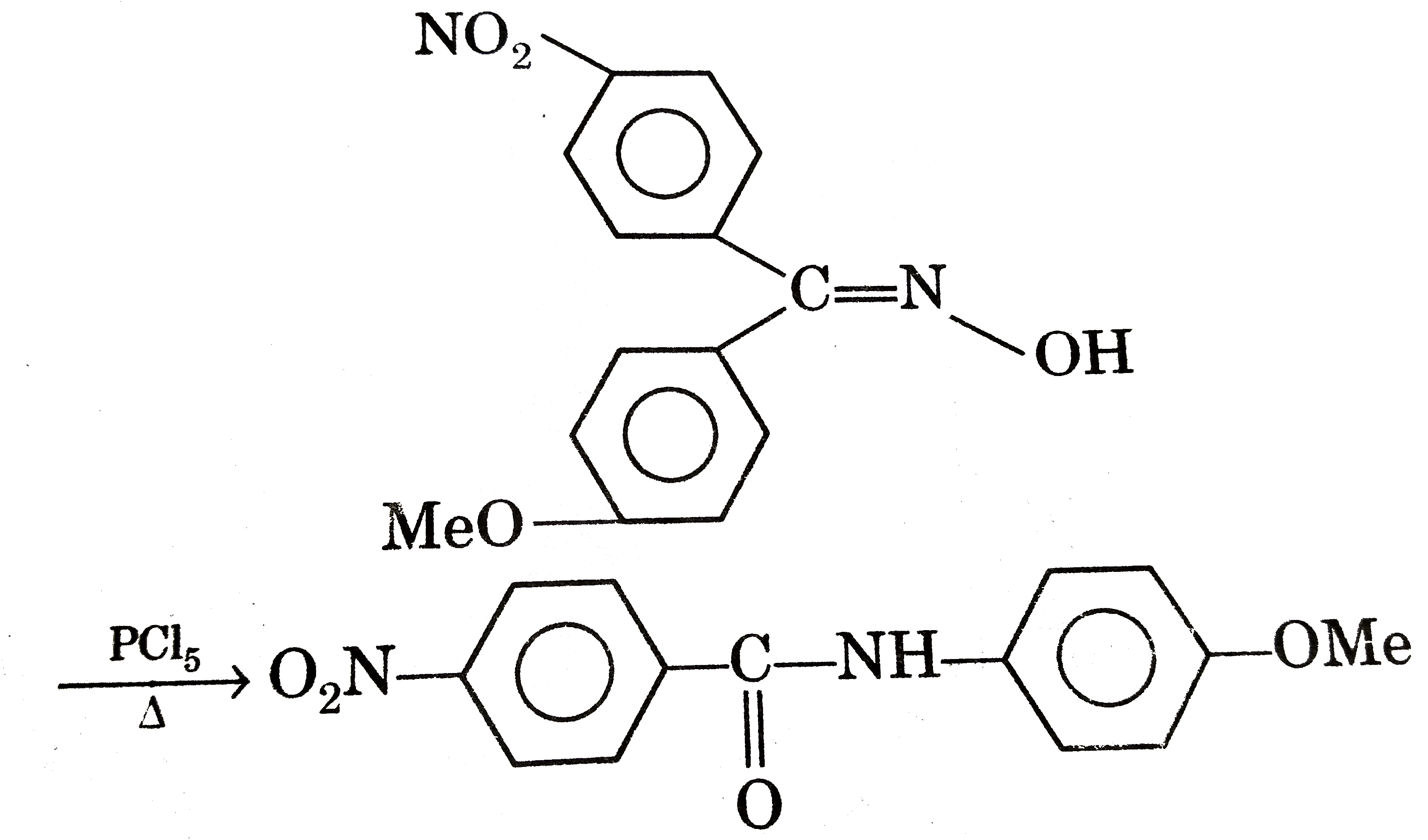
Statement -2: Migratory aptitude of p-methoxyphenyl group is greater than migratory aptitude p-nitrophenyl of group during carbrocation rearrangements.View Solution

