OA and OB are two perpendicular straight lines. A straight line AB is drawn in such a manner that OA+OB=8. Find the locus of the mid point of AB.
The correct Answer is:x+y=4
Step by step video, text & image solution for OA and OB are two perpendicular straight lines. A straight line AB is drawn in such a manner that OA+OB=8. Find the locus of the mid point of AB. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES Book:ARIHANT MATHSChapter:COORDINATE SYSTEM AND COORDINATES Exercise:Exercise (Single Option Correct Type Questions)
Explore 15 Videos
- COORDINATE SYSTEM AND COORDINATES Book:ARIHANT MATHSChapter:COORDINATE SYSTEM AND COORDINATES Exercise:Exercise (More Than One Correct Option Type Questions)
Explore 7 Videos
- COORDINATE SYSTEM AND COORDINATES Book:ARIHANT MATHSChapter:COORDINATE SYSTEM AND COORDINATES Exercise:Exercise For Session 3
Explore 19 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:ARIHANT MATHSChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 20 Videos
- DEFINITE INTEGRALBook:ARIHANT MATHSChapter:DEFINITE INTEGRALExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
Knowledge Check
A straight line through the point (1,1) meets the x-axis at 'A' and the y axis at 'B'. The locus of the mid point of AB is :
A2xy + x + y = 0Bx + y - 2xy = 0Cx + y + 2 = 0Dx + y - 2 = 0A straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
A2xy+x+y=0Bx+y-2y=0Cx+y+2=0Dx+y-2=0An ellipse slides between two perpendicular lines the locus of its centre , is
AcircleBparabolaCellipseDhyperbola
The straight line passing through the point (8, 4) and cuts the y-axis at B and x-axis at A. The locus of middle point of AB is
View SolutionIn a figure , AB is a straight line , Find (x+y):
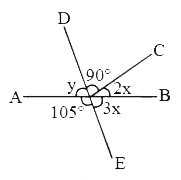
View SolutionThe straight line xa+yb=1 cuts the axes in A and B and a line perpendicular to AB cuts the axes in P and Q. Find the locus of the point of intersection of AQ and BP .
View SolutionA variable line is drawn through the origin O. Two points A and B same side of O are taken on the line such that OA=1 and OB=2 unit. . Through points A and B two lines are drawn making equal angle α with the line AB. Then the locus of the point of intersection of the lines, is:
View SolutionThe graph between the displacement x and time t for a particle moving in a straight line is shown in the figure. During the interval OA,AB,BC and CD the acceleration of the particle is
OA,AB,BC,CD
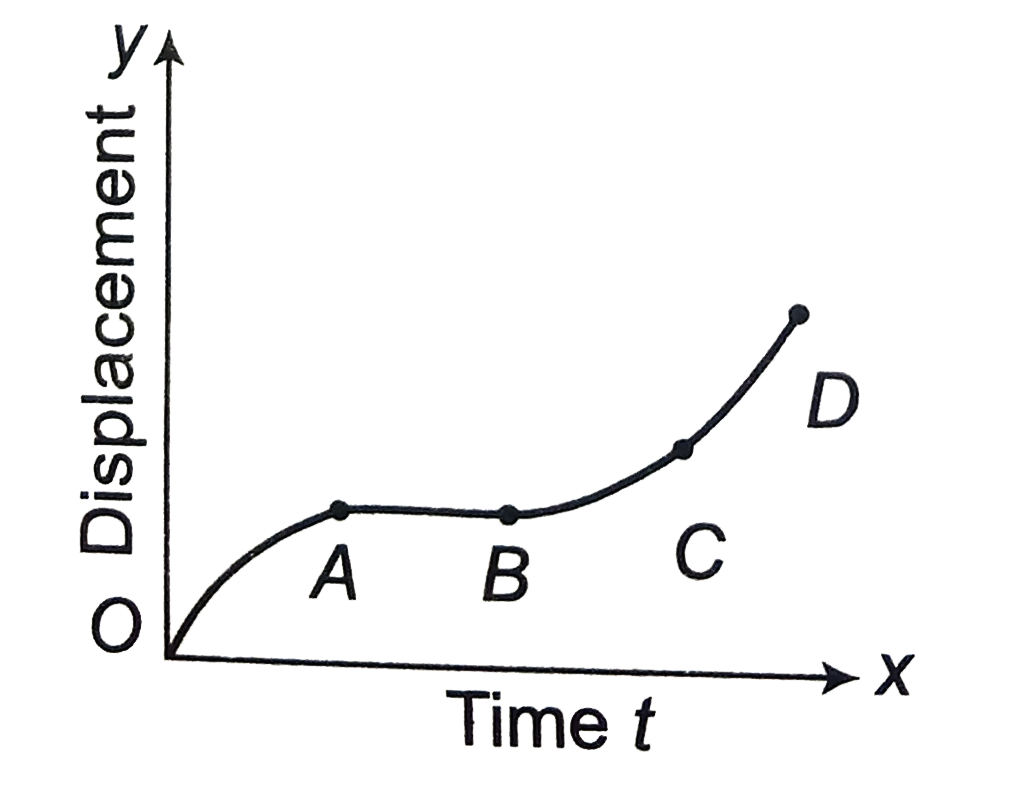
View Solution

