A, B, C and D are four points in space. Using vector methods, prove that AC2+BD2+AC2+BC2≥AB2+CD2 what is the implication of the sign of equality.
AB2+CD2
1AB2−1CD2
1CD2−1AB2
None of these
The correct Answer is:(a)
Step by step video, text & image solution for A, B, C and D are four points in space. Using vector methods, prove that AC^(2)+BD^(2)+AC^(2)+BC^(2)geAB^(2)+CD^(2) what is the implication of the sign of equality. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHSChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Exercise (More Than One Correct Option Type Questions)
Explore 28 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHSChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Exercise (Statement I And Ii Type Questions)
Explore 14 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHSChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Exercise For Session 4
Explore 7 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 35 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBook:ARIHANT MATHSChapter:TRIGONOMETRIC EQUATIONS AND INEQUATIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 12 Videos
Similar Questions
In fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
View SolutionIf AD is the median of △ABC, using vectors, prove that AB2+AC2=2(AD2+CD2)
View SolutionABCD is a rhombus. Prove that AB2+BC2+CD2+DA2=AC2+BD2
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2
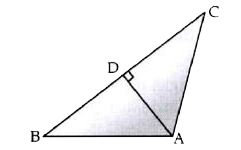
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionA, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View SolutionUsing vector method prove that in any triangle ABCa2=b2+c2−2bccosA.
View SolutionIn ABC , AD is perpendicular to BC . Prove that: AB2+CD2=AC2+BD2 (ii) AB2−BD2=AC2−CD2
View SolutionIn a quadrilateral ABCD, ∠A+∠D=90∘. Prove that AC2+BD2=AD2+BC2.
View Solution

