मान लीजिए कि ω एक (यूनिटी) का घनमूल है और ω≠1 है । मान लीजिए P और Q, ω और ω2 द्वारा परिभाषित सम्मिश्र समतल पर बिंदु हैं । यदि O मूलबिंदु है, तो OP और OQ के बीच का कोण क्या हैं?
60∘
90∘
120∘
150∘
The correct Answer is:A
हम जानते हैं की, इकाई का nवां मूल सम बहुभुज के शीर्षों को सम्मिश्र (आर्गेन्ड) असमतल पर दर्शाता है ।
जो इकाई त्रिज्या के वृत के अन्तर्गत होता है ।
∵ω तथा ω2 समबाहु त्रिभुज के शीर्ष को दर्शाता है ।
∴ अभीष्ट कोण =60∘
Topper's Solved these Questions
- सम्मिश्र संख्याएँ Book:NDA PATHFINDERChapter:सम्मिश्र संख्याएँ Exercise:अभ्यास प्रश्नावली
Explore 90 Videos
- समुच्चय सिद्धान्तBook:NDA PATHFINDERChapter:समुच्चय सिद्धान्तExercise:विगत वर्षो के प्रश्न
Explore 29 Videos
- सांख्यिकीBook:NDA PATHFINDERChapter:सांख्यिकीExercise:विगत वर्षो के प्रश्न
Explore 59 Videos
Similar Questions
(i5+i6+i7+i8+i9)(1+i) का मान है
View Solutionयदि A कोई B समुच्चय हो तो A∩(A∪B) किसके बराबर है ?
View Solutionआँकड़ो 20,20,20,21,21,21,21,21,22,22,22,22,22,22,22,23,23,23,23,23,24,24 तथा 25 का बहुलक क्या है?
View Solutionयदि 1,ω,ω2 इकाई एक घनमूल हों, तो ∣∣∣1ωω−ω∣∣∣ का मान होगा -
View Solutionयदि w इकाई का एक घनमूल हो तो सारणिक ∣∣ ∣ ∣∣1w4w8w4w81w81w4∣∣ ∣ ∣∣का मान है-
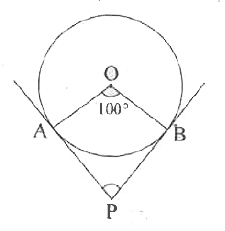
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
View Solutionयदि ω इकाई का एक घनमूल हो, तो सारणिक ∣∣ ∣ ∣∣1ω4ω8ω4ω81ω81ω4∣∣ ∣ ∣∣ का मान है-
View Solutionयदि ω इकाई का घनमूल हो तो सारणिक ∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣ का मान ज्ञात कीजिए |
View Solutionयदि ω इकाई का एक काल्पनिक घन मूल है, तो सारणिक ∣∣ ∣ ∣∣1+ωω2−ω1+ω2ω−ω2ω+ω2ω−ω2∣∣ ∣ ∣∣ का मान है-
View Solutionयदि ω(≠1) इकाई का घनमूल है और (1+ω)7=A+Bω हो, तो A और B क्रमशः होंगे
View Solutionमाना z और w दो अशून्य सम्मिश्र संख्याएँ इस प्रकार है कि |z|=|w| और कोणांक (z) + कोणांक (w)=π, तब z बराबर होगा |
View Solutionयदि ω इकाई का घनमूल है, तो (1+ω−ω2)2+(1−ω+ω2)2+1 का मान होगा
View Solutionयदि समतल x+2y+kz=0 और 2x+y-2z=0 लंबवत है, तो k का मान है
View Solutionव्यंजक 1.(2−ω)(2−ω2)+2.(3−ω)(3−ω2)+.......+(n−1)(n−ω)(n−ω2), जहाँ ω एक इकाई का काल्पनिक घनमूल है, का मान है।
View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"sec A का मान-1 और 1 के बीच में होता है
View Solutionयदि 1,omega,omega^2 इकाई के घनमूल हों, तो |(1,omega),(omega,-omega)| का मान होगा :
View Solution

