A wire of density 9×103kg/m3 is stretched between two clamps 1 m apart and is stretched to an extension of 4.9×10−4 metre.Young's modulus of material is 9×1010N/m2.Then
The lowest frequency of standing wave is 35 Hz
The frquency of 1st overtone is 70 Hz
The frequency of 1st overtone is 105 Hz
The stress in the wire is 4.41×107N/m2
Speed of wave in wire V=√TρA=√YΔllA×1ρA=√YΔllp
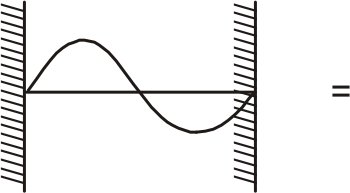
Maximum time period means minimum frequency , that means fundamental mode.
f=Vλ=V2l
∴T=2lV=2l√lpYΔl=135 second
∴(f=35Hz)
and , frequency of first overtone =Vl= 70 Hz
Topper's Solved these Questions
Similar Questions
A wire of density 9000kg/m3 is stretched between two clamps 100cm apart while subjected to an extension od 0.05cm. What is the lowest frequency of transverse vibrations in the wire , assuming Young's modulus of the material to be 9×1010N/m2?
View SolutionA wire of density 9000kgm−3 is stretched two clamps 2 m apart and its length increase by 0.05 cm. Calculate the frequecny of the fundamental trasverse vibration of the srting .(y of the material of wire 9×1010N/m2)
hint: Calculate tension of the wire from formula, young's modulus =stressstrain
View Solution
Knowledge Check
A wire of density 9×103kg/m3 is stretched between two clamps 1 m apart and is stretched to an extension of 4.9×10−4 metre.Young's modulus of material is 9×1010N/m2.Then
AThe lowest frequency of standing wave is 35HzBThe frequency of 1st overtone is 70HzCThe frequency of 1st overtone is 105HzDThe stress in the wire is 4.41×107N/m2A wire of density 9×103kg/m3 is stretched between two clamps 1 m apart and is subjected to an extension of 4.9×10−4m. The lowest frequency of transverse vibration in the wire is (Y=9×1010N/m2)
A40HzB35HzC30HzD25HzA wire of density 9gm/cm3 is stretched between two clamps 1.00m apart while subjected to an extension of 0.05cm. The lowest frequency of transverse vibration in the wire is (Assume Young's modulus Y=9×1010N/m2).
A35HzB45HzC75HzD90Hz
Calculate the percentage increase in length of a wire of diameter 2.2 mm stretched by a load of 100 kg. Young's modulus of wire is 12.5×1010 N m−2.
View SolutionA copper wire of length 4.0mm and area of cross-section 1.2cm2 is stretched with a force of 4.8×103N. If Young's modulus for copper is 1.2×1011N/m2, the increases in the length of the wire will be
View SolutionA metal wire is observed to stretch by one part in a million when subjected to a stress of 8×104N/m2. The Young's modulus of the metal is
View SolutionA body of mass 3.14kg is suspended from one end of a wire of length 10m. The radius of cross-section of the wire is changing uniformly from 5×10−4m at the top (i.e. point of suspension) to 9.8×10−4m at the bottom . Young's modulus of elasticity is 2×1011N/m2. The change in length of the wire is
View SolutionA wire of length 10 m and cross-section are 10−6m2 is stretched with a force of 20 N. If the elongation is 1 mm, the Young's modulus of material of the wire will be
View Solution

