Figure shows the adiabatic curve for $n$ moles of an ideal gas, the bulk modulus for the gas corresponding to the point $P$ will be

A

$n R (1 + \frac{2 T_{0}}{V_{0}})$

B

$n R (2 + \frac{T_{0}}{V_{0}}$

C

$n R (1 + \frac{T_{0}}{V_{0}}$

D

$n R (1 + \frac{T_{0}}{2 V_{0}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Bulk's modulus $K = \frac{- d p}{d V / V} = g a,, a P [P V^{γ} = c o n s tan t)$
For the curve $T V^{γ - 1} = k$ (constant)
or $V d T + T (γ - 1) d V = 0$
or $\frac{d V}{d T} = \frac{- V}{(γ - 1) T} = - 1$
$∴ Γ = 1 + \frac{V_{0}}{T_{0}}$
$∴ K = γ [\frac{n R T_{0}}{V_{0}}] = n R (1 + \frac{T_{0}}{V_{0}})$ .

|

Updated on:21/07/2023

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For two mole of an ideal gas :
A $C_{v} - C_{p} = R$
B $C_{p} - C_{v} = 2 R$
C $C_{p} - C_{v} = R$
D $C_{v} - C_{p} = 2 R$
Question 2 - Select One or More
During an adiabatic reversibly expansion of an ideal gas
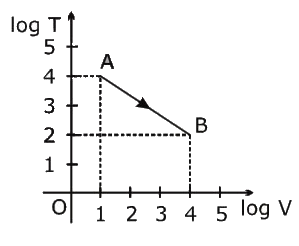
Ainternal energy of the system decreases
Btemperature of the system decreases
Cthe value of y changes
Dpressure increases
Question 3 - Select One
Figure shows the adiabatic curve on log-log scale performed on a ideal gas. The gas must be:-

AMonoatomic
BDiatomic
CA mixture of monoatomic and diatomic
DA mixture of diatomic and polyatomic

A2Z-KINETIC THEORY OF GASES AND THERMODYNAMICS-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile