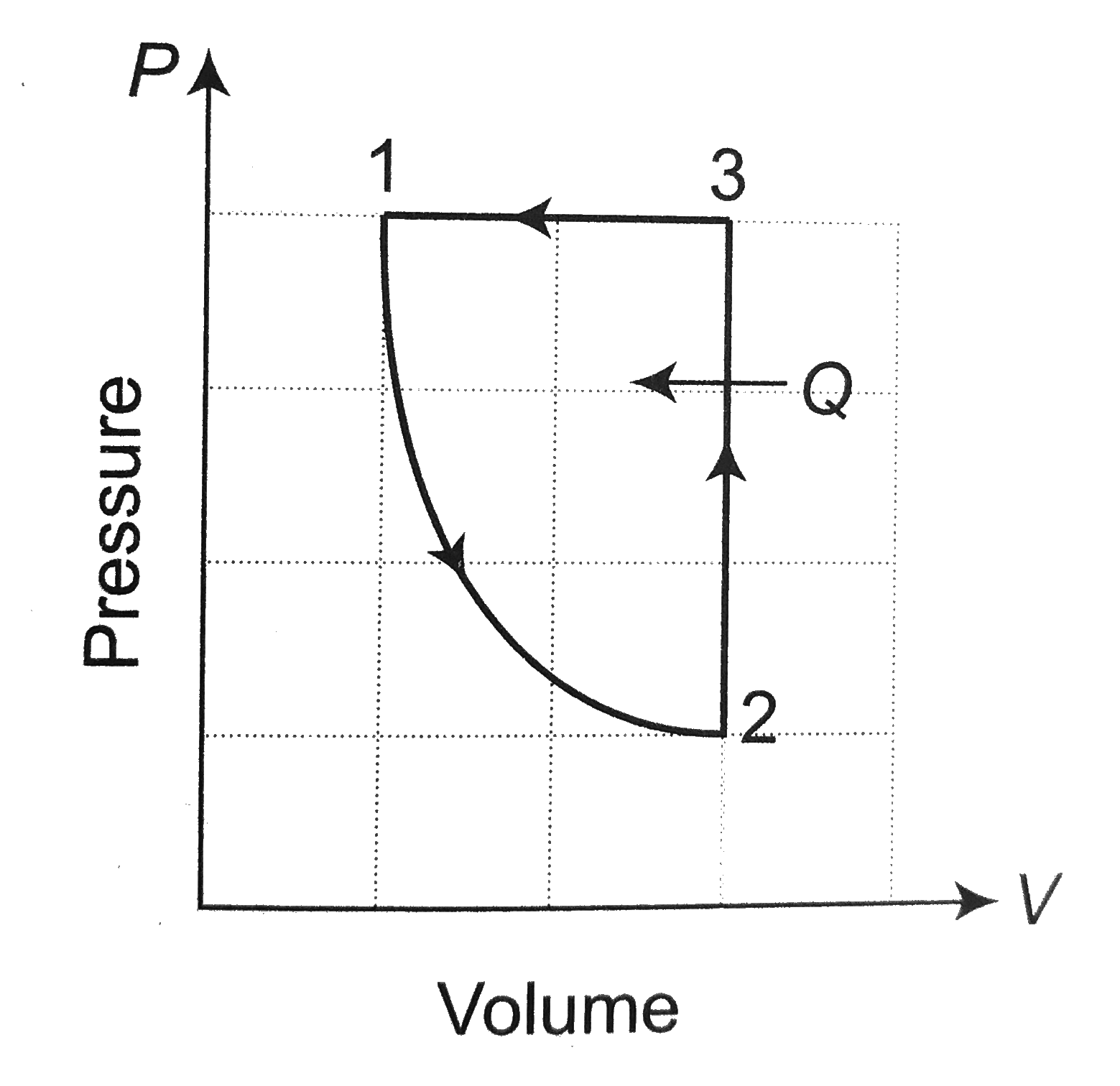
A sample of an ideal gas initially having internal energy U1 is allowed to expand adiabatically performing work W. Heat Q is then supplied to it, keeping the volume constant at its new value, until the pressure raised to its original value. The internal energy is then U3 (see figure). find the increase in internal energy (U3−U1)?
Q+W
Q−W
γW−Q
Q−γW
The correct Answer is:B
Process 1→2 is adiabatic
Q12=ΔU12+W12=>0=(U2−U1)+W
U2−U1=−W
Process 2→3 is isochoric
Q23=ΔU23+W23⇒Q=U3−U2
W23=0∴V=constant
⇒U3−U2=Q
Now (U3−U2)+(U2−U1)=U3−U1
⇒Q−W=U3−U1
⇒U3=Q+U1−W⇒U3−U1=Q−W.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Second Law Of Thermodynamics
29 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Problems Based On Mixed Concepts
49 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - First Law Of Thermodynamics , Internal Energy And Work Done
55 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
Similar Questions
One mole of a gas is allowed to expand adiabatically and irreversibly from a volume of 4 litres to a volume of 8 litres against the constant external pressure of one atm. Calculate internal energy change (ΔU) of system.
View SolutionWhen an ideal diatomic gas is heated at constant pressure fraction of the heat energy supplied which increases the internal energy of the gas is
View Solution
Knowledge Check
A monatomic gas expands at constant pressure on heating. The percentage of heat supplied that increases the internal energy of the gas and that is involed in the expansion is
A75%,25%B25%,75%C60%,40%D40%,60%Heat is supplied at constant pressure to diatomic gas. The part of this heat which goes to increase its internal energy will be
A57B3C25D23When an ideal diatomic gas is heated at constant pressure, the fraction of the heat energy supplied which increases the internal energy of the gas, is :
A25B35C37D57
A gas is allowed to expand in an insulated container against a constant external pressure of 3 atm from an initial volume of 5.0L to final volume of 9.0L .The change in internal energy ΔU of the gas is
View SolutionWhen an ideal monoatomic gas is heated at constant pressure,the fraction of heat energy supplied which increases internal energy of the gas is ?
View SolutionThe relation between internal energy U, pressure P and volume V of a gas in an adiabatic process is
U=a+bPV
where a and b are positive constants. What is the value of γ ?
View SolutionIf internal energy of gas is U=3PV+4 then the gas can be
View SolutionWhen an ideal diatomic gas is heated at constant pressure the fraction of the heat energy supplied which increases the internal energy of the gas is .
View Solution
