Two holes are made in the side of the tank such that the jets of water flowing out of them meet at the same point on the ground. If one hole is at a height of above the bottom, then the distance of the other holes from the top surface of water is
The correct Answer is:D
To solve the problem of determining the distance of the second hole from the top surface of water, we can follow these steps:
1. Understand the Setup:
We have a tank with two holes. One hole is located 3 cm above the bottom of the tank. We need to find the height of the second hole from the top surface of the water in the tank.
2. Define Variables:
- Let the total height of the tank be H.
- The height of the first hole from the bottom is h1=3cm.
- The height of the second hole from the bottom is h2.
- The height of the second hole from the top surface is H−h2.
3. Use the Principle of Equal Horizontal Range:
For the jets of water to meet at the same point on the ground, the horizontal ranges of the water jets from both holes must be equal. The horizontal range R for a hole at height h is given by:
R=v⋅t
where v is the velocity of efflux and t is the time of flight.
4. Calculate Velocity of Efflux:
The velocity of efflux from a hole at height h is given by:
v=√2gh
Thus, for the first hole:
v1=√2g(H−3)
For the second hole:
v2=√2gh2
5. Calculate Time of Flight:
The time of flight for a jet of water falling from a height h is given by:
t=√2hg
Thus, for the first hole:
t1=√2⋅3g=√6g
For the second hole:
t2=√2h2g
6. Set the Horizontal Ranges Equal:
Since the horizontal ranges must be equal:
v1⋅t1=v2⋅t2
Substituting the expressions for v and t:
√2g(H−3)⋅√6g=√2gh2⋅√2h2g
Simplifying this gives:
√12(H−3)=2h2
7. Solve for h2:
Squaring both sides:
12(H−3)=4h22
Rearranging gives:
h22=3(H−3)
Taking the square root:
h2=√3(H−3)
8. Determine the Distance from the Top Surface:
The distance from the top surface of the water is:
H−h2=H−√3(H−3)
9. Conclusion:
Since we are looking for the specific case where both holes are symmetrically placed, we can conclude that if one hole is 3 cm from the bottom, the other hole must also be 3 cm from the top surface of the water. Therefore, the distance of the second hole from the top surface of water is:
H−h2=3cm
Final Answer:
The distance of the second hole from the top surface of water is 3 cm.
We have a tank with two holes. One hole is located 3 cm above the bottom of the tank. We need to find the height of the second hole from the top surface of the water in the tank.
- Let the total height of the tank be H.
- The height of the first hole from the bottom is h1=3cm.
- The height of the second hole from the bottom is h2.
- The height of the second hole from the top surface is H−h2.
For the jets of water to meet at the same point on the ground, the horizontal ranges of the water jets from both holes must be equal. The horizontal range R for a hole at height h is given by:
R=v⋅t
where v is the velocity of efflux and t is the time of flight.
The velocity of efflux from a hole at height h is given by:
v=√2gh
Thus, for the first hole:
v1=√2g(H−3)
For the second hole:
v2=√2gh2
The time of flight for a jet of water falling from a height h is given by:
t=√2hg
Thus, for the first hole:
t1=√2⋅3g=√6g
For the second hole:
t2=√2h2g
Since the horizontal ranges must be equal:
v1⋅t1=v2⋅t2
Substituting the expressions for v and t:
√2g(H−3)⋅√6g=√2gh2⋅√2h2g
Simplifying this gives:
√12(H−3)=2h2
Squaring both sides:
12(H−3)=4h22
Rearranging gives:
h22=3(H−3)
Taking the square root:
h2=√3(H−3)
The distance from the top surface of the water is:
H−h2=H−√3(H−3)
Since we are looking for the specific case where both holes are symmetrically placed, we can conclude that if one hole is 3 cm from the bottom, the other hole must also be 3 cm from the top surface of the water. Therefore, the distance of the second hole from the top surface of water is:
H−h2=3cm
The distance of the second hole from the top surface of water is 3 cm.
Topper's Solved these Questions
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Problems Based On Mixed Concepts
Explore 29 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Assertion Reasoning
Explore 15 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Continuity Equation And Bernoulli'S Theorem
Explore 32 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
A stream of water escapes from a hole 2m above the base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View SolutionA stream of water escapes from a hole 2m above the Q. 1 base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View Solution
Knowledge Check
A tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
A2H√3B√3H2C√3HD3H4A hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2A tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)
A stream of water escapes from a hole 2m above the Q. 1 base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View SolutionA cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
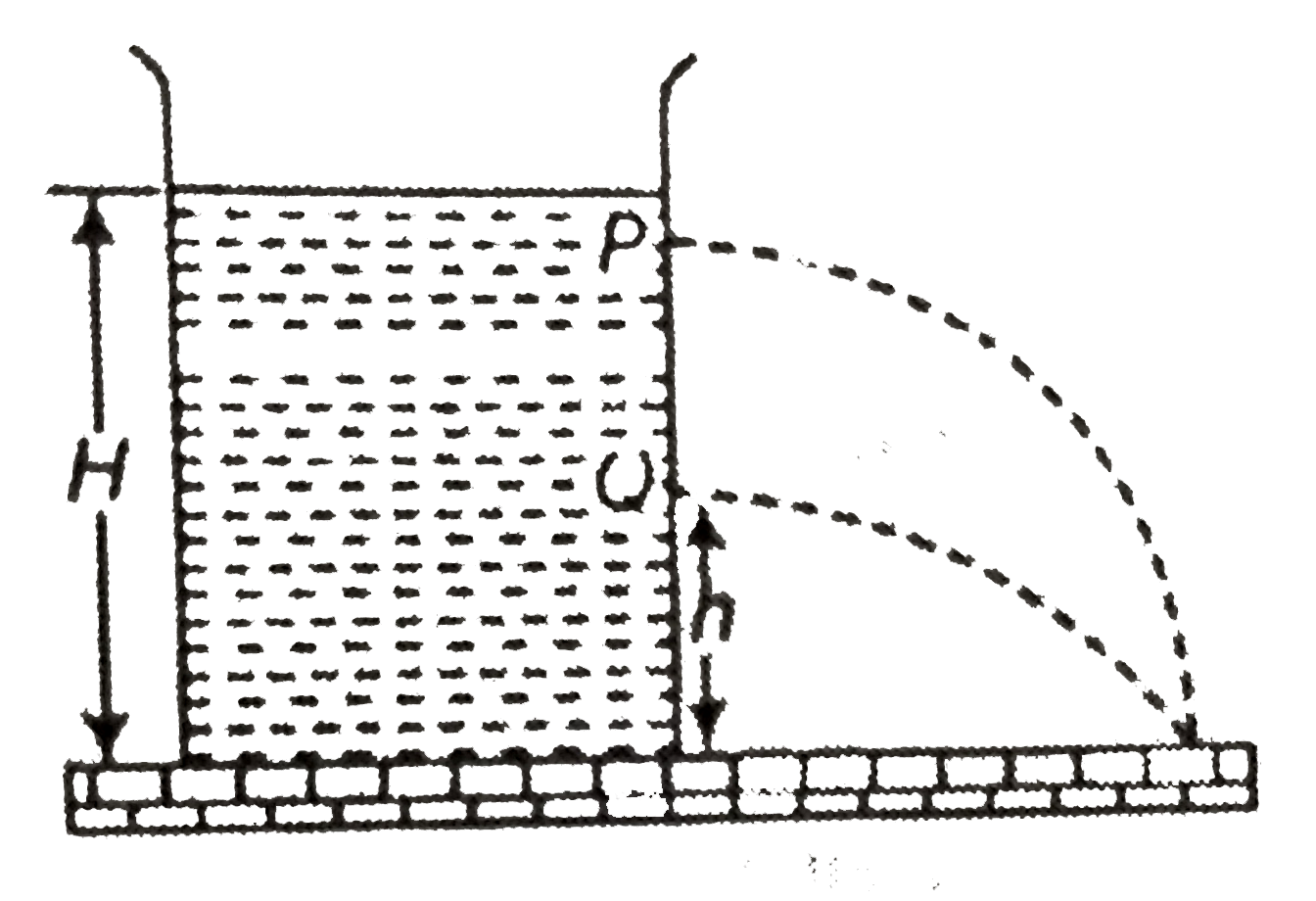
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View SolutionA cylindrical tank of height H is completely filled with water. On its vertical side there are two tiny holes, one above the middle at a height h1 and the other below the middle at a depth h2 If the jets of water from the holes meet at the same point at the horizontal plane through the bottom of the tank then the ratio h1/h2 is :
View SolutionA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
View Solution

