A rectangular block is 5 cm xx 5 cm xx 10 cm in size. The block floating in water change will occur in the level of water ?
no change
it will rise
it will fall
it may rise of fall depending on the density of block
The correct Answer is:A
To solve the problem of how the water level changes when a rectangular block is floating in water, we can follow these steps:
1. Identify the dimensions of the block:
The block has dimensions of 5 cm x 5 cm x 10 cm.
2. Understand the initial orientation:
Initially, the block is floating with its 5 cm side vertical. This means that the height of the block submerged in water is 5 cm.
3. Calculate the volume of the block:
The volume V of the rectangular block can be calculated using the formula for the volume of a rectangular prism:
V=length×width×height=5cm×5cm×10cm=250cm3
4. Determine the mass of the block:
The mass m of the block can be calculated if we know its density ρ. However, since the block is floating, we only need to know that the mass remains constant regardless of its orientation.
5. Understand the principle of flotation:
According to Archimedes' principle, the weight of the water displaced by the block is equal to the weight of the block. Since the block is floating, the volume of water displaced will remain constant as long as the mass of the block does not change.
6. Change the orientation of the block:
Now, the block is turned so that its 10 cm side is vertical. In this case, the height of the submerged part of the block will change.
7. Calculate the new submerged volume:
When the 10 cm side is vertical, the submerged height of the block will be different. However, the total volume of water displaced must remain the same because the mass of the block has not changed.
8. Conclusion on water level change:
Since the volume of water displaced remains constant regardless of the orientation of the block, the level of water will not change.
Final Answer:
There will be no change in the level of the water when the block is turned from having its 5 cm side vertical to having its 10 cm side vertical.
---
The block has dimensions of 5 cm x 5 cm x 10 cm.
Initially, the block is floating with its 5 cm side vertical. This means that the height of the block submerged in water is 5 cm.
The volume V of the rectangular block can be calculated using the formula for the volume of a rectangular prism:
V=length×width×height=5cm×5cm×10cm=250cm3
The mass m of the block can be calculated if we know its density ρ. However, since the block is floating, we only need to know that the mass remains constant regardless of its orientation.
According to Archimedes' principle, the weight of the water displaced by the block is equal to the weight of the block. Since the block is floating, the volume of water displaced will remain constant as long as the mass of the block does not change.
Now, the block is turned so that its 10 cm side is vertical. In this case, the height of the submerged part of the block will change.
When the 10 cm side is vertical, the submerged height of the block will be different. However, the total volume of water displaced must remain the same because the mass of the block has not changed.
Since the volume of water displaced remains constant regardless of the orientation of the block, the level of water will not change.
There will be no change in the level of the water when the block is turned from having its 5 cm side vertical to having its 10 cm side vertical.
Topper's Solved these Questions
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Continuity Equation And Bernoulli'S Theorem
Explore 32 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Application Of Bernoulli'S Theorem And Velocity Of Efflux
Explore 19 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Chapter Test
Explore 29 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
A cylindrical vessel of base radius 14 cm is filled with water to some height. If a rectangular solid of dimensions 22cm×7cm×5cm is immersed in it, what is the rise in water level ?
View SolutionA rectangular container whose base is a square of side 12 cm, contains sufficient water to submerge a rectangular solid 8cm×6cm×3cm. Find the rise in level of the water in the container when the solid is in it.
View Solution
Knowledge Check
A rectangular block is 5cm×5cm×10cm in size. The block is floating in water with 5 cm side vertical. If it floats with 10 cm side vertical, what change will occur in the level of water?
ANo changeBIt will riseCIt will fallDIt may rise or fall depending on the density of blockA rectangular wooden block 5cm×10cm×10cm in size is kept on a horizontal surface with its face of largest area on the surface. A minimum force of 1.5 N applied parallel to the surface sets the block in sliding motion along the surface. If the block is now kept with its face of smaller area in contact with the surface, the minimum force applied parallel to the surface, to set the block in motion, is
Agreater than 1.5 NBless than 1.5 NCequal to 1.5 NDmay be greater or less than 1.5 NIn the given figure from a cuboidal solid metallic block of dimensions 15cm×10cm×5cm a cylindrical hole of diamter 7 cm is drilled out . Find the suface area of the remaining block .
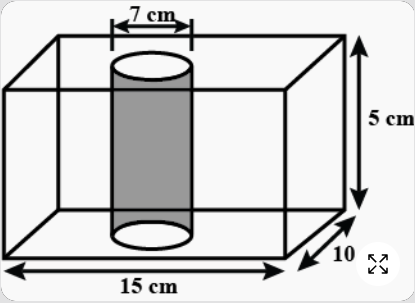 A450cm2B553cm2C550cm2D583cm2
A450cm2B553cm2C550cm2D583cm2
Sixteen glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions 20 cm × 10 cm × 10 cm and then the box is filled with water. Find the volume of water filled in the box.
View SolutionSixteen glass spheres each of radius 2 cm are paced into a cuboidal box of internal dimension 20cm×10cm×10cm and then the box is filled with water. Find the volume of water filled in the box
View SolutionA cylindrical vessel of base radius 14 cm is filled with water to some height. If a rectangular solid of dimensions 22 cm × 7 cm × 5 cm is immersed in it what is the rise in the water level ?
View SolutionA rectangular block of size 10cm×8cm×5cm is kept in three different positions P,Q and R in turns as shown in the figure. In each case, the shaded area is rigidly fixed and a definite force F is applied tangentially to the opposite face to deform the black. The displacement of the upper face will be

View SolutionA block of steel of size 5cm×5cm×5 cm is weighed in water. If the relative density of steel is
View Solution

