A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is $\frac{α}{R}$ from the center of the bigger disc. The value of $α$ is

A

$\frac{1}{4}$

B

$\frac{1}{3}$

C

$\frac{1}{2}$

D

$\frac{1}{6}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

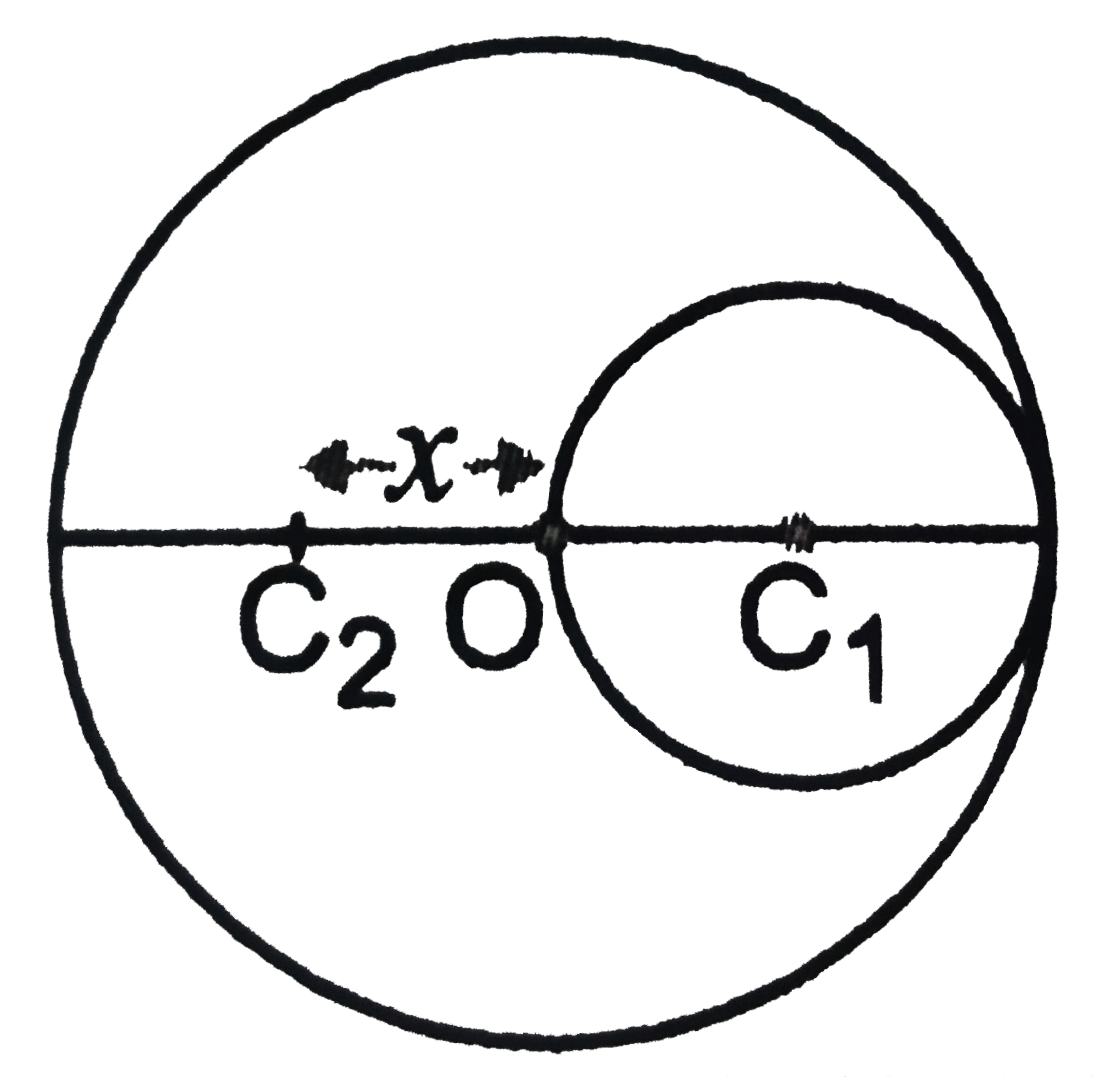
In Fig. $O$ is the centre of circular disc of radius $2 R$ and mass $M . C_{1}$ is centre of disc of radius $R$ , which is removed. If $ρ$ is mass per unit area of disc, then $M = π {(2 R)}^{2} ρ$
Mass of disc removed, $M_{1} = π (R^{2}) ρ = \frac{1}{4} M$
Mass of remaining disc, $M_{2} = M - M_{1}$
$= M - \frac{1}{4} M = \frac{3}{4} M$
Let centre of mass of remaining disc be at $C_{2}$ where $O C_{2} = x$
As $M_{1} \times O C_{1} = M_{2} \times O C_{2}$
$∴ \frac{M}{4} \times R = \frac{3 M}{4} x$
$x = \frac{R}{3} = α R ∴ α = \frac{1}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
A circular disc of radius $R$ is removed from a bigger circular disc of radius $2 R$ such that the circumferences of the discs coincide. The center of mass of new disc is $α R$ from the center of the bigger disc. The value of $α$ is
A $\frac{1}{3}$
B $\frac{1}{2}$
C $\frac{1}{6}$
D $\frac{1}{4}$
Question 2 - Select One
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is $α R$ from the centre of the bigger disc . the value of $α$ is
A $1 / 3$
B $1 / 2$
C $1 / 6$
D $1 / 4$
Question 3 - Select One
A circular disc of radius R is removed from a bigger circular dise of radius such that the circumferences of the discs coincide. The centre of mass of the new disc is $α R$ from the centre of the bigger disc. The value of a is:
A $\frac{1}{2}$
B $\frac{1}{6}$
C $\frac{1}{4}$
D $\frac{1}{3}$

Recommended Questions

Home
Ask Doubt
Profile